题目内容
定义域为R的偶函数f(x)满足对?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
考点:抽象函数及其应用,函数的零点
专题:计算题,函数的性质及应用
分析:令x=-1,求出f(1),可得函数f(x)的周期为2,当x∈[2,3]时,f(x)=-2x2+12x-18,画出图形,根据函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,利用数形结合的方法进行求解.
解答:
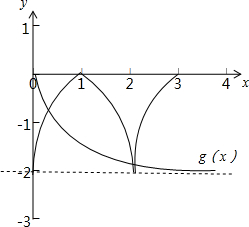 解:∵f(x+2)=f(x)-f(1),
解:∵f(x+2)=f(x)-f(1),
且f(x)是定义域为R的偶函数,
令x=-1可得f(-1+2)=f(-1)-f(1),
又f(-1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=-2x2+12x-18=-2(x-3)2,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=-2,
即loga3>-2,∴3<
,解得-
<a<
,又0<a<1,∴0<a<
,
故答案为:(0,
).
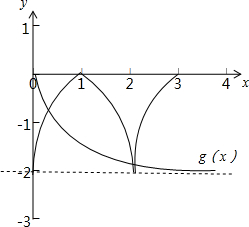 解:∵f(x+2)=f(x)-f(1),
解:∵f(x+2)=f(x)-f(1),且f(x)是定义域为R的偶函数,
令x=-1可得f(-1+2)=f(-1)-f(1),
又f(-1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=-2x2+12x-18=-2(x-3)2,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=-2,
即loga3>-2,∴3<
| 1 |
| a2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
故答案为:(0,
| ||
| 3 |
点评:此题主要考查函数奇偶性、周期性及其应用,解题的过程中用到了数形结合的方法,同时考查解决抽象函数的常用方法:赋值法,正确赋值是迅速解题的关键.

练习册系列答案
相关题目
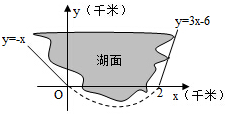 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )
如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
下列函数为奇函数的是( )
A、2x-
| ||
| B、x3sinx | ||
| C、2cosx+1 | ||
| D、x2+2x |
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时). 如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为
如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为