题目内容
在△ABC中,|
|=1,|
|=2且
与
的夹角为
,则BC边上的中线AD的长为 .
| AB |
| AC |
| AB |
| AC |
| π |
| 3 |
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:解三角形
分析:由余弦定理可得BC,再有勾股定理可判∠B=
,再由勾股定理可得结论.
| π |
| 2 |
解答:
解:如图,BC的中点为D,
由余弦定理可得BC2=12+22-2×1×2×cos
=3,
解得BC=
,∴AC2=AB2+BC2,△ABC为直角三角形,
∠B=
,在RT△ABD中,由勾股定理可得
AD2=AB2+BD2=12+(
)2=
,
∴AD=
故答案为:

由余弦定理可得BC2=12+22-2×1×2×cos
| π |
| 3 |
解得BC=
| 3 |
∠B=
| π |
| 2 |
AD2=AB2+BD2=12+(
| ||
| 2 |
| 7 |
| 4 |
∴AD=
| ||
| 2 |
故答案为:
| ||
| 2 |

点评:本题考查解三角形,涉及余弦定理和勾股定理得应用,属中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
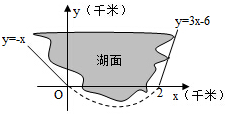 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )
如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
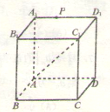 如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是
如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是