题目内容
14.在四面体ABCD中,AB⊥AD,AB=AD=BC=CD=1,且平面ABD⊥平面BCD,M为AB中点,则线段CM的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 如图所示,取BD的中点O,连接OA,OC,利用等腰三角形的性质可得OA⊥BD,OC⊥BD.又平面ABD⊥平面BCD,可得OA⊥平面BCD,OA⊥OC.建立空间直角坐标系.又AB⊥AD,可得DB=$\sqrt{2}$,取OB中点N,连结MN、CN,∴MN∥OA,MN⊥平面BCD.∴$CM=\sqrt{M{N}^{2}+M{N}^{2}}=\frac{\sqrt{3}}{2}$.
解答  解:如图所示,取BD的中点O,连接OA,OC,
解:如图所示,取BD的中点O,连接OA,OC,
∵AB=AD=BC=CD=1,∴OA⊥BD,OC⊥BD.
又平面ABD⊥平面BCD,∴OA⊥平面BCD,OA⊥OC.
又AB⊥AD,∴DB=$\sqrt{2}$.
取OB中点N,连结MN、CN,∴MN∥OA,MN⊥平面BCD.
∵MN2=ON2+OC2,
∴$CM=\sqrt{M{N}^{2}+M{N}^{2}}=\frac{\sqrt{3}}{2}$.
故选:C,
点评 本题考查了空间线面位置关系、向量夹角公式、等腰三角形的性质,考查了数形结合方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.为了得到函数$y=sin(2x+\frac{π}{3})$的图象,只需将函数y=sin2x的图象上每一点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
2.下列函数中为奇函数的是( )
| A. | y=xcosx | B. | y=xsinx | C. | y=|1nx| | D. | y=2-x |
9.已知集合A={x|$\frac{x-2}{x}$≤0},B={0,1,2,3},则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1} | D. | {1,2,3} |
19.二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
下面是z关于x的折线图:
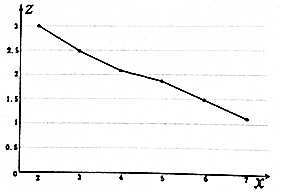
(1)由折线图可以看出,可以用线性回归模型拟合z与x的关系,请用相关数加以说明;
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?($\widehat{b}$、$\widehat{a}$小数点后保留两位有效数字).
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考公式:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$.
参考数据:
$\sum_{i=1}^{6}{x}_{i}{y}_{i}$=187.4,$\sum_{i=1}^{6}{x}_{i}{z}_{i}$=47.64,$\sum_{i=1}^{6}{{x}_{i}}^{2}$=139,$\sqrt{\sum_{i=1}^{6}({x}_{i}-\overline{x})^{2}}$=4.18,$\sqrt{\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}}$=13.96,
$\sqrt{\sum_{i=1}^{6}({z}_{i}-\overline{z})^{2}}$=1.53,ln1.46≈0.38,ln0.7118≈-0.34.
| 使用年数x | 2 | 3 | 4 | 5 | 6 | 7 |
| 售价y | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| z=lny | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |

(1)由折线图可以看出,可以用线性回归模型拟合z与x的关系,请用相关数加以说明;
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?($\widehat{b}$、$\widehat{a}$小数点后保留两位有效数字).
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考公式:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$.
参考数据:
$\sum_{i=1}^{6}{x}_{i}{y}_{i}$=187.4,$\sum_{i=1}^{6}{x}_{i}{z}_{i}$=47.64,$\sum_{i=1}^{6}{{x}_{i}}^{2}$=139,$\sqrt{\sum_{i=1}^{6}({x}_{i}-\overline{x})^{2}}$=4.18,$\sqrt{\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}}$=13.96,
$\sqrt{\sum_{i=1}^{6}({z}_{i}-\overline{z})^{2}}$=1.53,ln1.46≈0.38,ln0.7118≈-0.34.
6.对于数列{an},定义H0=$\frac{{{a_1}+2{a_2}+…+{2^{n-1}}{a_n}}}{n}$为{an}的“优值”.现已知某数列的“优值”H0=2n+1,记数列{an-20}的前n项和为Sn,则Sn的最小值为( )
| A. | -64 | B. | -68 | C. | -70 | D. | -72 |
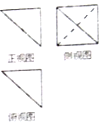 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.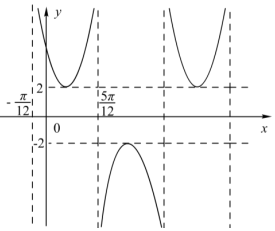 函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.
函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.