题目内容
2.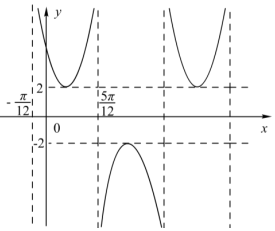 函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.
函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.
分析 由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,再代值计算即可.
解答 解:由图象可得到A=2,$\frac{T}{2}$=$\frac{5π}{12}$+$\frac{π}{12}$=$\frac{π}{2}$,
∴T=π,
∴ω=$\frac{2π}{π}$=2,
当x=$\frac{5π}{12}$-$\frac{π}{12}$=$\frac{π}{6}$时,f(x)=2,
∴$\frac{2}{sin(2x+φ)}$=2,
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∴f(x)=$\frac{2}{sin(2x+\frac{π}{6})}$,
∴f($\frac{π}{4}$)=$\frac{2}{sin(\frac{π}{2}+\frac{π}{6})}$=$\frac{4\sqrt{3}}{3}$,
故答案为:$\frac{4\sqrt{3}}{3}$
点评 本题主要考查利用图象特征,属于基础题.

练习册系列答案
相关题目
14.在四面体ABCD中,AB⊥AD,AB=AD=BC=CD=1,且平面ABD⊥平面BCD,M为AB中点,则线段CM的长为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
13. 如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{{\sqrt{30}}}{10}$ | B. | $\frac{{\sqrt{30}}}{15}$ | C. | $\frac{{\sqrt{30}}}{30}$ | D. | $\frac{{\sqrt{15}}}{15}$ |
7.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
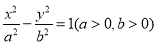 的左、右焦点分别为
的左、右焦点分别为 ,
, ,以
,以 为圆心,
为圆心, 为半径的圆与双曲线在第一、二象限内依次交于
为半径的圆与双曲线在第一、二象限内依次交于 ,
, 两点,若
两点,若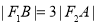 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )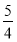 B.
B.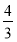 C.
C. D.2
D.2