题目内容
9.已知集合A={x|$\frac{x-2}{x}$≤0},B={0,1,2,3},则A∩B=( )| A. | {1,2} | B. | {0,1,2} | C. | {1} | D. | {1,2,3} |
分析 求出A中不等式的解集确定出A,找出A与B的交集即可.
解答 解:由A中不等式变形得:x(x-2)≤0且x≠0,
解得:0<x≤2,即A=(0,2],
∵B={0,1,2,3},
∴A∩B={1,2},
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
1.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系表:
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
| A. | $y=5+\frac{5}{2}sin\frac{π}{12}t,t∈[0,24]$ | B. | $y=5+\frac{5}{2}sin(\frac{π}{12}t+\frac{π}{2}),t∈[0,24]$ | ||
| C. | $y=5+\frac{5}{2}sin\frac{π}{6}t,t∈[0,24]$ | D. | $y=5+\frac{5}{2}sin(\frac{π}{6}t+π),t∈[0,24]$ |
17.已知复数z的实部为a(a<0),虚部为1,模长为2,$\overline{z}$是z的共轭复数,则$\frac{1+\sqrt{3}i}{\overline{z}}$的值为( )
| A. | $\frac{\sqrt{3}+i}{2}$ | B. | -$\sqrt{3}$-i | C. | -$\sqrt{3}$+i | D. | -$\frac{\sqrt{3}+i}{2}$ |
14.在四面体ABCD中,AB⊥AD,AB=AD=BC=CD=1,且平面ABD⊥平面BCD,M为AB中点,则线段CM的长为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.已知全集U=R,集合A={x|x>2},B={1,2,3,4},那么(∁UA)∩B=( )
| A. | {3,4} | B. | {1,2,3} | C. | {1,2} | D. | {1,2,3,4} |
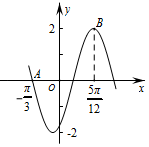 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).