题目内容
6.对于数列{an},定义H0=$\frac{{{a_1}+2{a_2}+…+{2^{n-1}}{a_n}}}{n}$为{an}的“优值”.现已知某数列的“优值”H0=2n+1,记数列{an-20}的前n项和为Sn,则Sn的最小值为( )| A. | -64 | B. | -68 | C. | -70 | D. | -72 |
分析 由{an}的“优值”的定义可知a1+2a2+…+2n-1•an=n•2n+1,当n≥2时,a1+2a2+…+2n-2•an-1=(n-1)•2n,则求得an=2(n+1),则an-20=2n-18,由数列的单调性可知当n=8或9时,{an-20}的前n项和为Sn,取最小值.
解答 解:由题意可知:H0=$\frac{{{a_1}+2{a_2}+…+{2^{n-1}}{a_n}}}{n}$=2n+1,
则a1+2a2+…+2n-1•an=n•2n+1,
当n≥2时,a1+2a2+…+2n-2•an-1=(n-1)•2n,
两式相减得:2n-1•an=n•2n+1-(n-1)•2n,
an=2(n+1),
当n=1时成立,
∴an-20=2n-18,当an-20≤0时,即n≤9时,
故当n=8或9时,{an-20}的前n项和为Sn,取最小值,
最小值为S8=S9=$\frac{9×(-16+0)}{2}$=-72,
故选D.
点评 本题考查等差数列的通项公式,数列与函数单调性的应用,考查计算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.已知复数z的实部为a(a<0),虚部为1,模长为2,$\overline{z}$是z的共轭复数,则$\frac{1+\sqrt{3}i}{\overline{z}}$的值为( )
| A. | $\frac{\sqrt{3}+i}{2}$ | B. | -$\sqrt{3}$-i | C. | -$\sqrt{3}$+i | D. | -$\frac{\sqrt{3}+i}{2}$ |
14.在四面体ABCD中,AB⊥AD,AB=AD=BC=CD=1,且平面ABD⊥平面BCD,M为AB中点,则线段CM的长为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.已知全集U=R,集合A={x|x>2},B={1,2,3,4},那么(∁UA)∩B=( )
| A. | {3,4} | B. | {1,2,3} | C. | {1,2} | D. | {1,2,3,4} |
13. 如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{{\sqrt{30}}}{10}$ | B. | $\frac{{\sqrt{30}}}{15}$ | C. | $\frac{{\sqrt{30}}}{30}$ | D. | $\frac{{\sqrt{15}}}{15}$ |
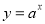 ,②
,② ,③
,③ ,④
,④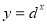 ,根据图象可得a、b、c、d与1的大小关系为( )
,根据图象可得a、b、c、d与1的大小关系为( )