题目内容
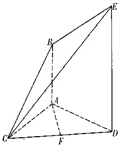 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)取EC中点G,连BG,GF,证明四边形ABGF为平行四边形,可得AF∥BG,利用线面平行的判定定理,即可得出结论;
(Ⅱ)证明BG⊥DE,BG⊥CD,可得BG⊥平面CDE,利用面面垂直的判定定理,即可得出结论
(Ⅱ)证明BG⊥DE,BG⊥CD,可得BG⊥平面CDE,利用面面垂直的判定定理,即可得出结论
解答:
 证明:(Ⅰ)取EC中点G,连BG,GF.
证明:(Ⅰ)取EC中点G,连BG,GF.
∵F是CD的中点,∴FG∥DE,且FG=
DE.
又∵AB∥DE,且AB=
DE.
∴四边形ABGF为平行四边形.
∴AF∥BG.
又BG?平面BCE,AF?平面BCE.
∴AF∥平面BCE.
(Ⅱ)∵AB⊥平面ACD,AF?平面ACD,
∴AB⊥AF.
∵AB∥DE,∴AF⊥DE.
又∵△ACD为正三角形,∴AF⊥CD.
∵BG∥AF,∴BG⊥DE,BG⊥CD.
∵CD∩DE=D,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.
 证明:(Ⅰ)取EC中点G,连BG,GF.
证明:(Ⅰ)取EC中点G,连BG,GF.∵F是CD的中点,∴FG∥DE,且FG=
| 1 |
| 2 |
又∵AB∥DE,且AB=
| 1 |
| 2 |
∴四边形ABGF为平行四边形.
∴AF∥BG.
又BG?平面BCE,AF?平面BCE.
∴AF∥平面BCE.
(Ⅱ)∵AB⊥平面ACD,AF?平面ACD,
∴AB⊥AF.
∵AB∥DE,∴AF⊥DE.
又∵△ACD为正三角形,∴AF⊥CD.
∵BG∥AF,∴BG⊥DE,BG⊥CD.
∵CD∩DE=D,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.
点评:本题考查线面平行,面面垂直,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知角α的终边经过点P(2,-1),则
=( )
| sinα-cosα |
| sinα+cosα |
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
下列说法正确的是( )
| A、函数f(x)=ax+1(a>0,且a≠1)的图象恒过定点(0,1) | ||
| B、函数f(x)=x-3在其定义域上是减函数 | ||
C、函数f(x)=2
| ||
| D、函数f(x)=|log2x|在区间(1,+∞)上单调递增 |
 已知函数:f(x)=lg|x|.请解答下列问题:
已知函数:f(x)=lg|x|.请解答下列问题: