题目内容
在数列{an}中,a1≠0,an+1=
an,Sn为{an}的前n项和.记Rn=
,则数列{Rn}的最大项为第 项.
| 3 |
| 82Sn-S2n |
| an+1 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:利用等比数列的通项公式及其前n项和公式可得Rn=
,再利用基本不等式的性质即可得出.
83-(3
| ||||||
|
解答:
解:∵a1≠0,an+1=
an,
∴an=a1(
)n-1=a1•3
,an+1=a1•3
.
Sn=
,S2n=
.
∴Rn=
=
=
≤
,
比较R3,R4,R5可得当n=4时,Rn取得最大值.
故答案为:4.
| 3 |
∴an=a1(
| 3 |
| n-1 |
| 2 |
| n |
| 2 |
Sn=
a1(3
| ||
|
| a1(3n-1) | ||
|
∴Rn=
| 82Sn-S2n |
| an+1 |
| ||||||||||
a1•3
|
83-(3
| ||||||
|
83-2
| ||
|
比较R3,R4,R5可得当n=4时,Rn取得最大值.
故答案为:4.
点评:本题考查了等比数列的通项公式及其前n项和公式、基本不等式的性质,考查了计算能力,属于中档题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设函数y=f(x)在区间(a,b)上的导函数为f′(x),f′(x)在区间(a,b)上的导函数为f″(x),若在区间(a,b)上f″(x)>0,则称函数f(x)在区间(a,b)上为“凹函数”,已知f(x)=
x5-
mx4-2x2在区间(1,3)上为“凹函数”,则实数m的取值范围为( )
| 1 |
| 20 |
| 1 |
| 12 |
A、(-∞,
| ||
B、[
| ||
| C、(-∞,-3) | ||
| D、(-∞,5] |
下列函数中,最小值为2的是( )
A、y=x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
| D、y=(x2+1)2+2 |
已知函数f(x)=ex,如果x1,x2∈R,且x1≠x2,下列关于f(x)的性质,其中正确的是( )
①(x1-x2)[f(x1)-f(x2)]>0;
②f(-x)=f(x);
③f(-x)=-f(x);
④
>f(
).
①(x1-x2)[f(x1)-f(x2)]>0;
②f(-x)=f(x);
③f(-x)=-f(x);
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| A、①② | B、①③ | C、②④ | D、①④ |
设f为(0,+∞)→(0,+∞)的函数,对任意正实数x,f(5x)=5f(x),f(x)=2-|x-3|,1≤x≤5,则使得f(x)=f(665)的最小实数x为( )
| A、45 | B、65 | C、85 | D、165 |
满足不等式a3>(-3)3的实数a的取值范围是( )
| A、(-3,+∞) |
| B、(-∞,-3) |
| C、(3,+∞) |
| D、(-3,3) |
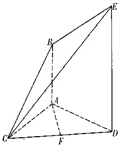 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.