题目内容
已知点P(-4,0)及圆C:x2+y2+6x-4y+4=0.
(Ⅰ)当直线l过点P且与圆心C的距离为l时,求直线l的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,当|AB|取得最小值时,求以线段AB为直径的圆的方程.
(Ⅰ)当直线l过点P且与圆心C的距离为l时,求直线l的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,当|AB|取得最小值时,求以线段AB为直径的圆的方程.
考点:直线与圆的位置关系
专题:综合题
分析:(Ⅰ)把圆的方程变为标准方程后,分两种情况①斜率k存在时,因为直线经过点P,设出直线的方程,利用点到直线的距离公式表示出圆心到所设直线的距离d,让d等于1列出关于k的方程,求出方程的解即可得到k的值,根据k的值和P的坐标写出直线l的方程即可;②当斜率不存在时显然得到直线l的方程为x=-4;
(Ⅱ)点P(-4,0)为AB的中点时,|AB|取得最小值,从而写出所求圆的标准方程即可.
(Ⅱ)点P(-4,0)为AB的中点时,|AB|取得最小值,从而写出所求圆的标准方程即可.
解答:
解:(Ⅰ)由题意知,圆的标准方程为:(x-3)2+(y+2)2=9,
①设直线l的斜率为k(k存在)
则方程为y-0=k(x+4)即kx-y+4k=0
又⊙C的圆心为(3,-2),r=3,
由
=1,得k=
所以直线方程为3x-4y+12=0;
②当k不存在时,直线l的方程为x=-4.
综上,直线l的方程为3x-4y+6=0或x=-4;
(Ⅱ)点P(-4,0)为AB的中点时,|AB|取得最小值,
∵|PC|=
,r=3,
∴|AB|min=2
=4,
∴以线段AB为直径的圆的方程为:(x+4)2+y2=4.
①设直线l的斜率为k(k存在)
则方程为y-0=k(x+4)即kx-y+4k=0
又⊙C的圆心为(3,-2),r=3,
由
| |-3k-2+4k| | ||
|
| 3 |
| 4 |
所以直线方程为3x-4y+12=0;
②当k不存在时,直线l的方程为x=-4.
综上,直线l的方程为3x-4y+6=0或x=-4;
(Ⅱ)点P(-4,0)为AB的中点时,|AB|取得最小值,
∵|PC|=
| 5 |
∴|AB|min=2
| 9-5 |
∴以线段AB为直径的圆的方程为:(x+4)2+y2=4.
点评:此题考查学生灵活运用点到直线的距离公式化简求值,灵活运用垂径定理及韦达定理化简求值,会根据圆心坐标和半径写出圆的标准方程,是一道中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
若不等式组
,表示的平面区域是一个钝角三角形,则实数k的取值范围为( )
|
| A、(0,1) |
| B、(-∞,-1)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、D(-1,0) |
设f为(0,+∞)→(0,+∞)的函数,对任意正实数x,f(5x)=5f(x),f(x)=2-|x-3|,1≤x≤5,则使得f(x)=f(665)的最小实数x为( )
| A、45 | B、65 | C、85 | D、165 |
若曲线y=
与直线kx-y+1=3k有交点,则k的取值范围是( )
| 1-x2 |
A、[0,
| ||
B、(-∞,0)∪[
| ||
C、(0,
| ||
D、(-∞,0))∪(
|
定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=2x-2-x+2,则f(2)等于( )
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
底面半径为1的圆锥侧面展开图是一个圆心角为直角的扇形,则该圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
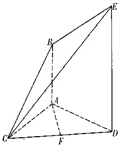 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.