题目内容
已知数列{an}为等差数列,且a1=1,S5=25,则{an}的通项公式an= .
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列的前n项和公式、性质求出a3的值,再由通项公式求出公差d和an.
解答:
解:因为数列{an}为等差数列,S5=25,
所以S5=
=25,则a3=5,
又a1=1,所以公差d=
=2,
所以an=a1+(n-1)d=2n-1,
故答案为:2n-1.
所以S5=
| 5(a1+a5) |
| 2 |
又a1=1,所以公差d=
| 5-1 |
| 2 |
所以an=a1+(n-1)d=2n-1,
故答案为:2n-1.
点评:本题考查了等差数列的前n项和公式、性质,以及通项公式的灵活应用,属于基础题.

练习册系列答案
相关题目
若曲线y=
与直线kx-y+1=3k有交点,则k的取值范围是( )
| 1-x2 |
A、[0,
| ||
B、(-∞,0)∪[
| ||
C、(0,
| ||
D、(-∞,0))∪(
|
定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=2x-2-x+2,则f(2)等于( )
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
函数y=2-x的反函数的图象为( )
A、 |
B、 |
C、 |
D、 |
满足不等式a3>(-3)3的实数a的取值范围是( )
| A、(-3,+∞) |
| B、(-∞,-3) |
| C、(3,+∞) |
| D、(-3,3) |
已知函数f(x)=sinx+acosx的图象关于直线x=
对称,且方程f(x)=m在[0,
)上恰有两个不同的实数根,则实数m取值范围是( )
| π |
| 6 |
| π |
| 2 |
| A、[0,1] | ||
| B、[1,2] | ||
C、[
| ||
D、[1,
|
底面半径为1的圆锥侧面展开图是一个圆心角为直角的扇形,则该圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
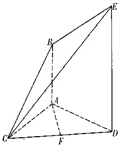 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.