题目内容
 已知函数:f(x)=lg|x|.请解答下列问题:
已知函数:f(x)=lg|x|.请解答下列问题:(1)判断函数f(x)的奇偶性;
(2)作出f(x)的大致图象并写出f(x)的单调递减区间;
(3)解方程:[f(x)]2-3f(x)-4=0.
考点:函数的图象
专题:函数的性质及应用
分析:(1)根据f(x)定义域为{x|x≠0},关于原点对称,且满足f(-x)=f(x),可得函数为偶函数.
(2)当x>0时,函数f(x)=lg|x|=lgx,当x<0时,函数f(x)的图象与x>0时的图象关于y轴对称,根据图象求得函数f(x)的单调区间.
(3)由[f(x)]2-3f(x)-4=0可得[f(x)+1][f(x)-4]=0.得f(x)=-1或f(x)=4,进而得出lg|x|=-1或lg|x|=4,再求x.
(2)当x>0时,函数f(x)=lg|x|=lgx,当x<0时,函数f(x)的图象与x>0时的图象关于y轴对称,根据图象求得函数f(x)的单调区间.
(3)由[f(x)]2-3f(x)-4=0可得[f(x)+1][f(x)-4]=0.得f(x)=-1或f(x)=4,进而得出lg|x|=-1或lg|x|=4,再求x.
解答:
解:(1)对于函数f(x)=lg|x|,定义域为{x|x≠0},关于原点对称,
且满足f(-x)=lg|-x|=lg|x|=f(x),
故函数为偶函数.
(2)当x>0时,函数f(x)=lg|x|=lgx,当x<0时,函数f(x)的图象与x>0时的图象关于y轴对称,图象如图:

显然(0,+∞)是f(x)在增区间,(-∞,0)是减区间.
(3)由[f(x)]2-3f(x)-4=0可得[f(x)+1][f(x)-4]=0.
∴f(x)=-1或f(x)=4
∴lg|x|=-1或lg|x|=4,
∴|x|=
或|x|=10000,
∴x=±
或x=±10000.
且满足f(-x)=lg|-x|=lg|x|=f(x),
故函数为偶函数.
(2)当x>0时,函数f(x)=lg|x|=lgx,当x<0时,函数f(x)的图象与x>0时的图象关于y轴对称,图象如图:

显然(0,+∞)是f(x)在增区间,(-∞,0)是减区间.
(3)由[f(x)]2-3f(x)-4=0可得[f(x)+1][f(x)-4]=0.
∴f(x)=-1或f(x)=4
∴lg|x|=-1或lg|x|=4,
∴|x|=
| 1 |
| 10 |
∴x=±
| 1 |
| 10 |
点评:本题主要考查对数函数的单调性,判断函数的奇偶性的方法,属于基础题.

练习册系列答案
相关题目
已知集合M={x|x2-1=0},则以下正确的是( )
| A、{1}∈M |
| B、-1∈M |
| C、∅∈M |
| D、{-1,1}?M |
已知向量
,
的夹角为120°,且|
|=1,|
|=2,则向量
-
在向量
+
上的投影是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、-3 |
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
设函数y=f(x)在区间(a,b)上的导函数为f′(x),f′(x)在区间(a,b)上的导函数为f″(x),若在区间(a,b)上f″(x)>0,则称函数f(x)在区间(a,b)上为“凹函数”,已知f(x)=
x5-
mx4-2x2在区间(1,3)上为“凹函数”,则实数m的取值范围为( )
| 1 |
| 20 |
| 1 |
| 12 |
A、(-∞,
| ||
B、[
| ||
| C、(-∞,-3) | ||
| D、(-∞,5] |
若不等式组
,表示的平面区域是一个钝角三角形,则实数k的取值范围为( )
|
| A、(0,1) |
| B、(-∞,-1)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、D(-1,0) |
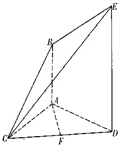 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.