题目内容

按照斜二测画法得到，一个平面图形的直观图为腰长为2的等腰直角三角形，则这一平面图形的面积为
 
．
考点：平面图形的直观图
专题：空间位置关系与距离
分析：可根据直观图和原图面积之间的比例关系
S原图
S直观图
=2
2
求解，这样计算出来比较简单，也可作出原图，直接求面积．
解答： 解：由题意，直观图的面积为
1
2
×2×2=2，
因为直观图和原图面积之间的关系为
S原图
S直观图
=2
2
，
故原△ABO的面积是4
2
，
故答案为：4
2
点评：本题考查斜二测画法及斜二测画法中原图和直观图面积之间的联系，考查作图能力和运算能力，是一个基础题．
练习册系列答案
相关题目
已知向量
a
，
b
的夹角为120°，且|
a
|=1，|
b
|=2，则向量
a
-
b
在向量
a
+
b
上的投影是（　　）
A、-
3
B、
3
C、
3
3
D、-3
定义在（0，
π
2
）上的函数f（x）满足f′（x）sinx-f（x）cosx＞0，设a=
2
3
3
f（
π
3
），b=
2
f（
π
4
），c=2f（
π
6
），则a，b，c的大小关系是
 
．
若不等式组
x-y+5≥0
y≥kx+5
0≤x≤2
，表示的平面区域是一个钝角三角形，则实数k的取值范围为（　　）
A、（0，1）
B、（-∞，-1）∪（0，1）
C、（-1，0）∪（1，+∞）
D、D（-1，0）
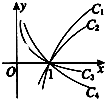已知函数C1：y=logax，C2=y=logbx，C3：y=logcx，C4：y=logdx在同一平面直角坐标系中的图象如图所示，其中a、b、c、d均为不等于1的整数，则a、b、c、d、1按从大到小的顺序为
 
（用“＜”号连接）
解下列关于x的不等式：
（1）（ax-2）（x+1）＞0；
（2）（1-ax）2＜1；
（3）12x2-ax＞a2．
符合下列条件的三角形有且只有一个的是（　　）
A、a=1，b=2，c=3
B、a=1，b=2，∠A=100°
C、a=1，b=
2
，∠A=30°
D、b=c=1，∠B=45°
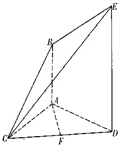如图，已知AB⊥平面ACD，DE∥AB，AC=AD=DE=2AB，且F是CD的中点．
（Ⅰ）求证：AF∥平面BCE；
（Ⅱ）求证：平面BCE⊥平面CDE．
若曲线y=
1-x2
与直线kx-y+1=3k有交点，则k的取值范围是（　　）
A、[0，
1
2
]
B、（-∞，0）∪[
1
2
，+∞）
C、（0，
1
2
）
D、（-∞，0））∪（
1
2
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网