题目内容
下列说法正确的是( )
| A、函数f(x)=ax+1(a>0,且a≠1)的图象恒过定点(0,1) | ||
| B、函数f(x)=x-3在其定义域上是减函数 | ||
C、函数f(x)=2
| ||
| D、函数f(x)=|log2x|在区间(1,+∞)上单调递增 |
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:由条件根据对数函数、指数函数、幂函数的单调性和特殊点,判断各个选项是否正确,从而得出结论.
解答:
解:由于当x=0时,函数f(x)=ax+1=2,故函数f(x)=ax+1的图象恒过定点(0,2),故A不正确.
由函数f(x)=x-3在的图象可得函数在(0,+∞)上单调递减,且f(x)>0,函数在(-∞,0)上单调递减,且f(x)<0,
故函数在其定义域内没有单调性,故B不正确.
由于函数f(x)=2
中,
≠0,故函数f(x)≠20,即f(x)≠1,故f(x)=2
值域一定不是(0,+∞),故C不正确.
在区间(1,+∞)上,函数f(x)=|log2x|=log2x,故函数在区间(1,+∞)上单调递增,故D正确,
故选:D.
由函数f(x)=x-3在的图象可得函数在(0,+∞)上单调递减,且f(x)>0,函数在(-∞,0)上单调递减,且f(x)<0,
故函数在其定义域内没有单调性,故B不正确.
由于函数f(x)=2
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
在区间(1,+∞)上,函数f(x)=|log2x|=log2x,故函数在区间(1,+∞)上单调递增,故D正确,
故选:D.
点评:本题主要考查对数函数、指数函数、幂函数的单调性和特殊点,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
符合下列条件的三角形有且只有一个的是( )
| A、a=1,b=2,c=3 | ||
| B、a=1,b=2,∠A=100° | ||
C、a=1,b=
| ||
| D、b=c=1,∠B=45° |
数列3,7,13,21,31,…的一个通项公式是( )
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n(n2-1) |
函数f(x)=2-x的大致图象为( )
A、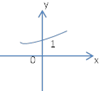 |
B、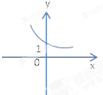 |
C、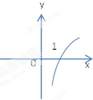 |
D、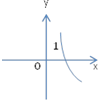 |
函数y=2-x的反函数的图象为( )
A、 |
B、 |
C、 |
D、 |
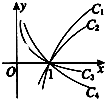 已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为
已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为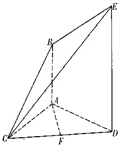 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.