题目内容
已知函数f(x)=a2x-2a+1.若命题“?x∈(0,1),f(x)≠0”是假命题,则实数a的取值范围是 .
考点:全称命题
专题:简易逻辑
分析:利用全称命题的否定是特称命题,通过特称命题是真命题,求出a的范围.
解答:
解:函数f(x)=a2x-2a+1,命题“?x∈(0,1),f(x)≠0”是假命题,
∴原命题的否定是:“存在实数x∈(0,1),使f(x)=0”是真命题,
∴f(1)f(0)<0,
即(a2-2a+1)(-2a+1)<0;
∴(a-1)2(2a-1)>0,
解得a>
,且a≠1;
∴实数a的取值范围是(
,1)∪(1,+∞).
故答案为:(
,1)∪(1,+∞).
∴原命题的否定是:“存在实数x∈(0,1),使f(x)=0”是真命题,
∴f(1)f(0)<0,
即(a2-2a+1)(-2a+1)<0;
∴(a-1)2(2a-1)>0,
解得a>
| 1 |
| 2 |
∴实数a的取值范围是(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查了命题的否定的应用问题,解题的关键是写出正确的全称命题,并且根据这个命题是一个假命题,得到正确的结论,是基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
符合下列条件的三角形有且只有一个的是( )
| A、a=1,b=2,c=3 | ||
| B、a=1,b=2,∠A=100° | ||
C、a=1,b=
| ||
| D、b=c=1,∠B=45° |
函数f(x)=2-x的大致图象为( )
A、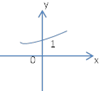 |
B、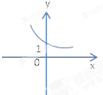 |
C、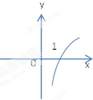 |
D、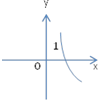 |
若曲线y=
与直线kx-y+1=3k有交点,则k的取值范围是( )
| 1-x2 |
A、[0,
| ||
B、(-∞,0)∪[
| ||
C、(0,
| ||
D、(-∞,0))∪(
|
已知函数f(x)=sinx+acosx的图象关于直线x=
对称,且方程f(x)=m在[0,
)上恰有两个不同的实数根,则实数m取值范围是( )
| π |
| 6 |
| π |
| 2 |
| A、[0,1] | ||
| B、[1,2] | ||
C、[
| ||
D、[1,
|
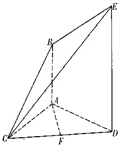 如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.