题目内容
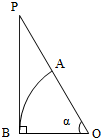 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧 |
| AB |
| α |
| tanα |
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:设出扇形的半径,求出扇形的面积,再在直角三角形中求出高PB,计算直角三角形的面积,由条件建立等式,解此等式求出tanα与α的关系,即可得出结论.
解答:
解:设扇形的半径为r,
则扇形的面积为
α r2,直角三角形POB中,PB=rtanα,
△POB的面积为
r×rtanα,由题意得
r×rtanα=2×
α r2,
∴tanα=2α,
∴
=
.
故答案为:
.
则扇形的面积为
| 1 |
| 2 |
△POB的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴tanα=2α,
∴
| α |
| tanα |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查扇形的面积公式及三角形的面积公式的应用,考查学生的计算能力,属于基础题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥ax-2,则a的取值范围是( )
|
| A、[-2,2] | ||
| B、[-2,0] | ||
C、[1-2
| ||
D、[1-2
|
已知正数a,b满足:三数a,1,b的倒数成等差数列,则a+b的最小值为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=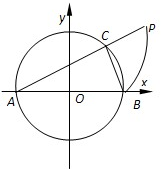 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )