题目内容
某名学生在连续五次考试中数学成绩与物理成绩如下:
(Ⅰ)用茎叶图表示数学成绩与物理成绩;
(Ⅱ)数学成绩为x,物理成绩为y,求变量x与y之间的回归直线方程.
(注:
=
=
,
=
-
)
| 数学(x) | 70 | 75 | 80 | 85 | 90 |
| 物理(y) | 60 | 65 | 70 | 75 | 80 |
(Ⅱ)数学成绩为x,物理成绩为y,求变量x与y之间的回归直线方程.
(注:
 |
| b |
| |||||||
|
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
考点:线性回归方程,茎叶图
专题:概率与统计
分析:(Ⅰ)根据所给数据,可用茎叶图表示数学成绩与物理成绩;
(Ⅱ)利用公式,求出相应系数,即可求变量x与y之间的回归直线方程.
(Ⅱ)利用公式,求出相应系数,即可求变量x与y之间的回归直线方程.
解答:
解:(Ⅰ)茎叶图如图所示
数学 物理
6 0 5
5 0 7 0 5
5 0 8
0 9
(Ⅱ)∵
xi2=32250,
xiyi=28250,
=80,
=70,(
)2=6400,(
)2=5600,∴
=
=1,
=
-
=-10,
∴所求回归直线方程为
=x-10.
数学 物理
6 0 5
5 0 7 0 5
5 0 8
0 9
(Ⅱ)∵
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
 |
| b |
| 28250-5×5600 |
| 32250-5×6400 |
 |
| a |
. |
| y |
 |
| b |
. |
| x |
∴所求回归直线方程为
 |
| y |
点评:本题考查茎叶图,考查回归直线方程,考查学生的计算能力,正确运用公式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
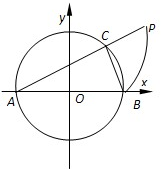 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
曲线y=x-
在点(1,0)处的切线方程为( )
| 1 |
| x |
| A、y=2x-2 |
| B、y=x-1 |
| C、y=0 |
| D、y=-x+1 |
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|