题目内容
已知直线y=ex+1与曲线y=ex+a相切(e是自然对数的底数),则a的值是( )
| A、e | ||
B、
| ||
| C、e+1 | ||
| D、1 |
考点:利用导数研究曲线上某点切线方程
专题:计算题
分析:先求导函数,利用直线y=ex+1与曲线y=ex+a相切,可知切线的斜率为e,即切点处的函数值为e,再利用切点处的函数值相等,即可求出a的值
解答:
解:设切点为(x,y)
∵y=ex+a,∴y′=ex+a
∴ex+a=e,即x+a=1,
又ex+a=ex+1,∴a=
故选B.
∵y=ex+a,∴y′=ex+a
∴ex+a=e,即x+a=1,
又ex+a=ex+1,∴a=
| 1 |
| e |
故选B.
点评:本题以直线与曲线相切为载体,考查了利用导数研究曲线上过某点切线方程的斜率,解题的关键是正确理解导数的几何意义.

练习册系列答案
相关题目
 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )| A、12π | B、18π |
| C、24π | D、30π |
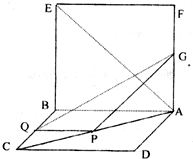 如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;
如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;