题目内容
已知实数x,y满足
,则z=-3x+2y的最大值为( )
|
| A、-4 | B、2 | C、4 | D、6 |
考点:简单线性规划
专题:不等式的解法及应用
分析:画出足约束条件
的平面区域,再将平面区域的各角点坐标代入进行判断,即可求出z=-3x+2y的最大值.
|
解答:
 解:已知实数x、y满足
解:已知实数x、y满足
,
在坐标系中画出可行域,如图中阴影三角形,
三个顶点分别是A(-2,0),B(2,2),C(0,-2).
可知,当x=-2,y=0,
z=-3x+2y的最大值是6.
故选D.
 解:已知实数x、y满足
解:已知实数x、y满足
|
在坐标系中画出可行域,如图中阴影三角形,
三个顶点分别是A(-2,0),B(2,2),C(0,-2).
可知,当x=-2,y=0,
z=-3x+2y的最大值是6.
故选D.
点评:本题考查线性规划问题,难度较小.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图所示,程序框图输出的值为( )


| A、12 | B、13 | C、14 | D、16 |
若双曲线
-
=1(a>0,b>0)的渐近线方程为y=±
x,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
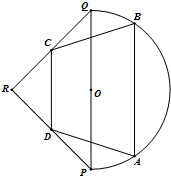 如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.
如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.