��Ŀ����
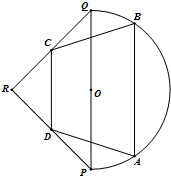 ��ͼ��������һ������������һ��ֱ��Ϊ2km�İ�Բ��һ����PQΪб�ߵĵ���ֱ�������Ρ�PRQ���ɣ�����OΪPQ���е㣮�����ڹ��ィ��һ���ı��ν����ܵ�ABCD����ʵ����Ҫ���ı���ABCD����������C��D�ֱ����߶�QR��PR�ϣ�������������A��B�ڰ�Բ�ϣ�AB��CD��PQ����AB��CD��ľ���Ϊ1km�����ı���ABCD���ܳ�Ϊckm��
��ͼ��������һ������������һ��ֱ��Ϊ2km�İ�Բ��һ����PQΪб�ߵĵ���ֱ�������Ρ�PRQ���ɣ�����OΪPQ���е㣮�����ڹ��ィ��һ���ı��ν����ܵ�ABCD����ʵ����Ҫ���ı���ABCD����������C��D�ֱ����߶�QR��PR�ϣ�������������A��B�ڰ�Բ�ϣ�AB��CD��PQ����AB��CD��ľ���Ϊ1km�����ı���ABCD���ܳ�Ϊckm����1����C��D�ֱ�ΪQR��PR���е㣬��AB����
��2�����ܳ�c�����ֵ��
���㣺���Ǻ�������ֵ,��ʵ�������н������Ǻ���ģ��
ר�⣺������,Ӧ����,���������ʼ�Ӧ��,���Ǻ�������ֵ
��������1������RO���ӳ��ֱ�AB��CD��M��N������OB�����õ���ֱ�������ε����ʣ�
��Ϲ��ɶ������㼴�ɵõ�AB�ij���
��2�����BOM=�ȣ��ɽ�ֱ�������οɵ�BM��OM�����ɵõ�c=AB+CD+BC+AD=2��sin��+cos��+
����
����
��
�����ҽ���a=bȡ�õȺţ������㼴�ɵõ����ֵ��
��Ϲ��ɶ������㼴�ɵõ�AB�ij���
��2�����BOM=�ȣ��ɽ�ֱ�������οɵ�BM��OM�����ɵõ�c=AB+CD+BC+AD=2��sin��+cos��+
| 1+(sin��-cos��)2 |
����
| a+b |
| 2 |
|
���
 ��1���⣺����RO���ӳ��ֱ�AB��CD��M��N������OB��
��1���⣺����RO���ӳ��ֱ�AB��CD��M��N������OB��
��C��D�ֱ�ΪQR��PR���е㣬PQ=2����CD=
PQ=1��
�ߡ�PRQΪ����ֱ�������Σ�PQΪб�ߣ���RO=
PQ=1��NO=
RO=
��
��MN=1����MO=
��
��Rt��BMO��BO=1����BM=
=
��
��AB=2BM=
����������������������
��2�����BOM=�ȣ�0���ȣ�
��
��Rt��BMO�У�BO=1����BM=sin�ȣ�OM=cos�ȣ�
��MN=1����CN=RN=1-ON=OM=cos�ȣ�
��BC=AD=
��
��c=AB+CD+BC+AD=2(sin��+cos��+
)����2
=2
��
��sin��+cos��=
������sin2��=
��
����=
��
ʱȡ�Ⱥţ�
�൱��=
����=
ʱ���ܳ�c�����ֵΪ2
km��
 ��1���⣺����RO���ӳ��ֱ�AB��CD��M��N������OB��
��1���⣺����RO���ӳ��ֱ�AB��CD��M��N������OB����C��D�ֱ�ΪQR��PR���е㣬PQ=2����CD=
| 1 |
| 2 |
�ߡ�PRQΪ����ֱ�������Σ�PQΪб�ߣ���RO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��MN=1����MO=
| 1 |
| 2 |
��Rt��BMO��BO=1����BM=
| BO2-OM2 |
| ||
| 2 |
��AB=2BM=
| 3 |
��2�����BOM=�ȣ�0���ȣ�
| �� |
| 2 |
��Rt��BMO�У�BO=1����BM=sin�ȣ�OM=cos�ȣ�
��MN=1����CN=RN=1-ON=OM=cos�ȣ�
��BC=AD=
| 1+(sin��-cos��)2 |
��c=AB+CD+BC+AD=2(sin��+cos��+
| 1+(sin��-cos��)2 |
| 2 |
(sin��+cos��)2+(
|
| 6 |
��sin��+cos��=
| 1+(sin��-cos��)2 |
| 1 |
| 2 |
����=
| �� |
| 12 |
| 5�� |
| 12 |
�൱��=
| �� |
| 12 |
| 5�� |
| 12 |
| 6 |
���������⿼�����Ǻ�������ֵ��������Ҫ����ʽ�����ã�����ͬ�ǵ�ƽ����ϵ���������������������е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
˫����
-
=1��a��0��b��0���Ľ�������������y=x2+1 ���У����˫���ߵ������ʵ��ڣ�������
| y2 |
| a2 |
| x2 |
| b2 |
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
������y2=2x���߷����ǣ�������
A��x=-
| ||
| B��x=-1 | ||
C��y=-
| ||
| D��y=-1 |
��֪ʵ��x��y����
����z=-3x+2y�����ֵΪ��������
|
| A��-4 | B��2 | C��4 | D��6 |