题目内容
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围为( )
| x |
A、0<k≤
| ||||||
B、0<k≤
| ||||||
C、0<k<
| ||||||
D、0<k<
|
考点:函数奇偶性的性质,函数的周期性
专题:函数的性质及应用
分析:在同一坐标系内作出y=f(x)图象和动直线l:y=kx+k,观察直线l可得:当已知方程有4个零点时直线l的活动范围应该在图中两条虚线之间,从而通过求直线斜率得到k取值范围.
解答:
解:∵偶函数f(x)当x∈[0,1]时,f(x)=
,
∴当x∈[-1,0]时图象与x∈[0,1]时关于y轴对称,
故x∈[-1,0]时f(x)=-
,
又∵f(x)是以2为周期的函数,
∴将函数f(x)在[-1,1]上的图象向左和向右平移2的整数倍个单位,可得f(x)在R上的图象.
∵直线l:y=kx+k经过定点(-1,0),斜率为k
∴直线l的图象是经过定点(-1,0)的动直线.(如图)
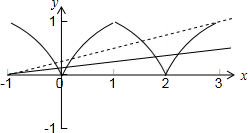
在同一坐标系内作出y=f(x)和动直线l:y=kx+k,当它们有4个公共点时,
方程f(x)=kx+k(k∈R,且k≠1)有4个根,
由两条虚线的斜率k1=0,k2=
,
故直线l的斜率0<k≤
,
故选:B
| x |
∴当x∈[-1,0]时图象与x∈[0,1]时关于y轴对称,
故x∈[-1,0]时f(x)=-
| x |
又∵f(x)是以2为周期的函数,
∴将函数f(x)在[-1,1]上的图象向左和向右平移2的整数倍个单位,可得f(x)在R上的图象.
∵直线l:y=kx+k经过定点(-1,0),斜率为k
∴直线l的图象是经过定点(-1,0)的动直线.(如图)

在同一坐标系内作出y=f(x)和动直线l:y=kx+k,当它们有4个公共点时,
方程f(x)=kx+k(k∈R,且k≠1)有4个根,
由两条虚线的斜率k1=0,k2=
| 1 |
| 4 |
故直线l的斜率0<k≤
| 1 |
| 4 |
故选:B
点评:本题给出已知函数图象与动直线有4个公共点,求斜率k的取值范围,着重考查了函数的周期性、奇偶性和直线的斜率等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
阅读程序框图,若输入m=1,n=2,则输出n=( )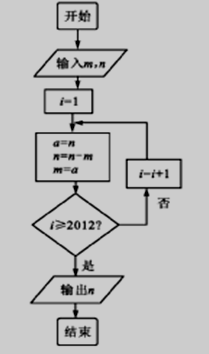

| A、1 | B、-1 | C、2 | D、-2 |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、16+8π |
| B、8+8π |
| C、16+16π |
| D、8+16π |
执行如图程序框图,那么输出S的值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|