题目内容
已知函数f(x)=
+sin(2x+
).
(1)求f(
)的值;
(2)求f(x)的单调递增区间.
sin(x-3π)cos(x+
| ||
| tan(π-x) |
| π |
| 3 |
(1)求f(
| π |
| 12 |
(2)求f(x)的单调递增区间.
考点:运用诱导公式化简求值,正弦函数的单调性
专题:三角函数的求值
分析:(1)由条件利用诱导公式求得f(x)=-
sin2x+sin(2x+
),从而求得f(
)的值.
(2)进一步化简函数的解析式为f(x)=
cos2x,再根据余弦函数的增区间求得f(x)的单调递增区间.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 12 |
(2)进一步化简函数的解析式为f(x)=
| ||
| 2 |
解答:
解:(1)由于函数f(x)=
+sin(2x+
)=
+sin(2x+
)=
+sin(2x+
)
=-sinxcosx+sin(2x+
)=-
sin2x+sin(2x+
),
∴f(
)=-
sin
+sin
=-
+1=
.
(2)由于f(x)=-
sin2x+sin(2x+
)=-
sin2x+sin2xcos
+cos2xsin
=
cos2x,
令2kπ-π≤2x≤2kπ,k∈z,求得kπ-
≤x≤kπ,故f(x)的增区间为[kπ-
,kπ],k∈z.
sin(x-3π)cos(x+
| ||
| tan(π-x) |
| π |
| 3 |
| -sin(3π-x)•(-sinx) |
| -tanx |
| π |
| 3 |
| sinx•sinx |
| -tanx |
| π |
| 3 |
=-sinxcosx+sin(2x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
∴f(
| π |
| 12 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
(2)由于f(x)=-
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
令2kπ-π≤2x≤2kπ,k∈z,求得kπ-
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,余弦函数的增区间,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是( )
某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是( )| A、5 | B、4 | C、3 | D、2 |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围为( )
| x |
A、0<k≤
| ||||||
B、0<k≤
| ||||||
C、0<k<
| ||||||
D、0<k<
|
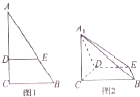 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.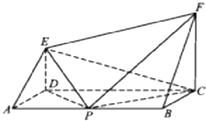 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题:
如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题: