题目内容
阅读程序框图,若输入m=1,n=2,则输出n=( )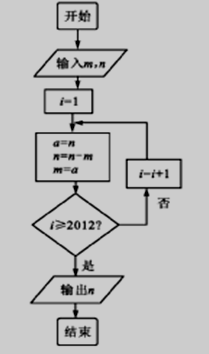

| A、1 | B、-1 | C、2 | D、-2 |
考点:程序框图
专题:算法和程序框图
分析:执行程序框图,依次写出每次循环得到的i,a,n,m的值,当i=2012,a=1,n=-1,m=1时,满足条件i≥2012,退出循环,输出n的值为-1.
解答:
解:执行程序框图,有
m=1,n=2,i=1
a=2,n=1,m=2
不满足条件i≥2012,i=2,a=1,n=-1,m=1
不满足条件i≥2012,i=3,a=-1,n=-2,m=-1
不满足条件i≥2012,i=4,a=-2,n=-1,m=-2
不满足条件i≥2012,i=5,a=-1,n=1,m=-1
不满足条件i≥2012,i=6,a=1,n=2,m=1
不满足条件i≥2012,i=7,a=2,n=1,m=2
不满足条件i≥2012,i=8,a=1,n=-1,m=1
不满足条件i≥2012,i=9,a=-1,n=-2,m=-1
不满足条件i≥2012,i=10,a=-2,n=-1,m=-2
不满足条件i≥2012,i=11,a=-1,n=1,m=-1
不满足条件i≥2012,i=12,a=1,n=2,m=1
不满足条件i≥2012,i=13,a=2,n=1,m=2
…
观察规律可知,n的取值周期为6,
由2011=6*335+1可知
不满足条件i≥2012,i=2011,a=2,n=1,m=2
不满足条件i≥2012,i=2012,a=1,n=-1,m=1
满足条件i≥2012,退出循环,输出n的值为-1.
故选:B.
m=1,n=2,i=1
a=2,n=1,m=2
不满足条件i≥2012,i=2,a=1,n=-1,m=1
不满足条件i≥2012,i=3,a=-1,n=-2,m=-1
不满足条件i≥2012,i=4,a=-2,n=-1,m=-2
不满足条件i≥2012,i=5,a=-1,n=1,m=-1
不满足条件i≥2012,i=6,a=1,n=2,m=1
不满足条件i≥2012,i=7,a=2,n=1,m=2
不满足条件i≥2012,i=8,a=1,n=-1,m=1
不满足条件i≥2012,i=9,a=-1,n=-2,m=-1
不满足条件i≥2012,i=10,a=-2,n=-1,m=-2
不满足条件i≥2012,i=11,a=-1,n=1,m=-1
不满足条件i≥2012,i=12,a=1,n=2,m=1
不满足条件i≥2012,i=13,a=2,n=1,m=2
…
观察规律可知,n的取值周期为6,
由2011=6*335+1可知
不满足条件i≥2012,i=2011,a=2,n=1,m=2
不满足条件i≥2012,i=2012,a=1,n=-1,m=1
满足条件i≥2012,退出循环,输出n的值为-1.
故选:B.
点评:本题主要考查了算法和程序框图,观察规律求得n的取值周期为6,从而周期得到退出循环时n的取值是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) 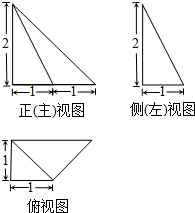

A、最长棱的棱长为
| ||
| B、最长棱的棱长为3 | ||
| C、侧面四个三角形中有且仅有一个是正三角形 | ||
| D、侧面四个三角形都是直角三角形 |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围为( )
| x |
A、0<k≤
| ||||||
B、0<k≤
| ||||||
C、0<k<
| ||||||
D、0<k<
|
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A、(-∞,-1] |
| B、(-∞,-1) |
| C、[-1,+∞) |
| D、(-1,+∞) |
执行如图所示的程序框图,输出的x值为( )


| A、4 | B、5 | C、6 | D、7 |