题目内容
设函数f(x)=
+b,其中a>0,b∈R,e=2.71828…为自然对数的底数.
(1)若函数f(x)在点(0,f(0))处的切线为直线l,证明:f(x)=
+b的图象恒在切线l的下方(除切点外).
(2)当a=1,设函数F(x)=f(x)-|lnx|,若?x0∈(0,+∞),使得F(x0)=0,求实数b的最小值.
| ax |
| e2x |
(1)若函数f(x)在点(0,f(0))处的切线为直线l,证明:f(x)=
| ax |
| e2x |
(2)当a=1,设函数F(x)=f(x)-|lnx|,若?x0∈(0,+∞),使得F(x0)=0,求实数b的最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=
,从而求出切线方程y=ax+b;再作差(
+b)-(ax+b)=ax(
-1),从而证明恒小于0即可;
(2)由题意,F(x)=f(x)-|lnx|=
+b-|lnx|.从而讨论去绝对值号,再求导确定函数的单调性,从而求最值,从而讨论最值的取值即可.
| a(1-2x) |
| e2x |
| ax |
| e2x |
| 1 |
| e2x |
(2)由题意,F(x)=f(x)-|lnx|=
| x |
| e2x |
解答:
解:(1)证明:由已知f′(x)=
,所以f′(0)=a;又∵f(0)=b;
所以切线l的方程为:y=ax+b;
又(
+b)-(ax+b)=ax(
-1),
因为a>0,当x>0时,
<1,
所以(
+b)-(ax+b)=ax(
-1)<0;
当x<0时,
>1,
所以(
+b)-(ax+b)=ax(
-1)<0;
故函数f(x)=
+b的图象恒在切线l的下方(除切点外);
(2)由题意,F(x)=f(x)-|lnx|=
+b-|lnx|.
①当0<x<1时,F(x)=
+b+lnx,
所以F′(x)=
+
=
;
在0<x<1时,函数y=e2x的值域为(1,e2),函数y=2x2-x的值域为(-
,1),
所以在0<x<1时,恒有2x2-x<e2x,即e2x+x-2x>0,
所以y=F(x)对任意x∈(0,1)大于零恒成立,
所以F(x)在(0,1)上单调递增;
②当x≥1时,F(x)=
+b-lnx,
F′(x)=
-
=
,
显然在x≥1时有函数y=x-2x2=x(1-2x)<0恒成立,
所以F′(x)<0对任意x∈(1,+∞)恒成立,
所以F(x)在(1,+∞)上单调递减;
由①②得,函数F(x)=
+b-|lnx|在(0,1)上单调递增,在(1,+∞)上单调递减,
所以F(x)的最大值为F(1)=
+b;
当
+b=0,即b=-
时,函数y=f(x)-|lnx|有且只有一个零点;
当
+b>0,即b>-
时,函数y=f(x)-|lnx|有两个不等的零点;
当
+b<0,即b<-
时,函数y=f(x)-|lnx|没有零点.
故若?x0∈(0,+∞),使得F(x0)=0,
则b≥-
,
所以b的最小值为-
.
| a(1-2x) |
| e2x |
所以切线l的方程为:y=ax+b;
又(
| ax |
| e2x |
| 1 |
| e2x |
因为a>0,当x>0时,
| 1 |
| e2x |
所以(
| ax |
| e2x |
| 1 |
| e2x |
当x<0时,
| 1 |
| e2x |
所以(
| 1 |
| e2x |
| 1 |
| e2x |
故函数f(x)=
| ax |
| e2x |
(2)由题意,F(x)=f(x)-|lnx|=
| x |
| e2x |
①当0<x<1时,F(x)=
| x |
| e2x |
所以F′(x)=
| 1-2x |
| e2x |
| 1 |
| x |
| x-2x2+e2x |
| xe2x |
在0<x<1时,函数y=e2x的值域为(1,e2),函数y=2x2-x的值域为(-
| 1 |
| 8 |
所以在0<x<1时,恒有2x2-x<e2x,即e2x+x-2x>0,
所以y=F(x)对任意x∈(0,1)大于零恒成立,
所以F(x)在(0,1)上单调递增;
②当x≥1时,F(x)=
| x |
| e2x |
F′(x)=
| 1-2x |
| e2x |
| 1 |
| x |
| x-2x2-e2x |
| xe2x |
显然在x≥1时有函数y=x-2x2=x(1-2x)<0恒成立,
所以F′(x)<0对任意x∈(1,+∞)恒成立,
所以F(x)在(1,+∞)上单调递减;
由①②得,函数F(x)=
| x |
| e2x |
所以F(x)的最大值为F(1)=
| 1 |
| e2 |
当
| 1 |
| e2 |
| 1 |
| e2 |
当
| 1 |
| e2 |
| 1 |
| e2 |
当
| 1 |
| e2 |
| 1 |
| e2 |
故若?x0∈(0,+∞),使得F(x0)=0,
则b≥-
| 1 |
| e2 |
所以b的最小值为-
| 1 |
| e2 |
点评:本题考查了导数的综合应用及分类讨论的数学思想应用,属于中档题.

练习册系列答案
相关题目
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围为( )
| x |
A、0<k≤
| ||||||
B、0<k≤
| ||||||
C、0<k<
| ||||||
D、0<k<
|
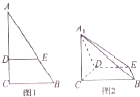 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.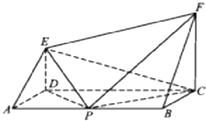 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题:
如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题: