题目内容
复数z=
的共轭复数在复平面上对应的点位于( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则、几何意义即可得出.
解答:
解:复数z=
=
=
的共轭复数为
-
i在复平面上对应的点为(
,-
)在第四象限.
故选:D.
| i |
| 1+i |
| i(1-i) |
| (1+i)(1-i) |
| i+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了复数的运算法则、几何意义,属于基础题.

练习册系列答案
相关题目
全集U={1,2,3,4,5,6},A={1,3},B={2,4},C={1,2,5,6},则(A∪B)∩∁UC=( )
| A、{1,2} |
| B、{3,4} |
| C、{1,2,3,4} |
| D、{3,4,5,6} |
设z=a+bi(a,b∈R),则z为纯虚数的必要不充分条件是( )
| A、a≠0且b=0 |
| B、a≠0且b≠0 |
| C、a=0 |
| D、a=0且b≠0 |
复数
的值是( )
| 1+i |
| 1-i |
| A、0 | B、1 | C、-1 | D、i |
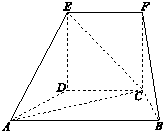 如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.
如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.