题目内容
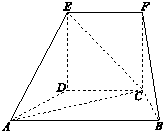 如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.
如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.(1)求BC与平面EAC所成角的正弦值;
(2)线段ED上是否存在点Q,使平面EAC⊥平面QBC?证明你的结论.
考点:平面与平面垂直的性质,直线与平面所成的角
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)首先通过运算找到CA,CF,CB两两互相垂直,然后建立空间直角坐标系,找到与平面EAC垂直的法向量,进一步利用向量的夹角求解,最后转化成正弦值.
(2)先假设点Q存在,然后利用反证法进行证明,通过向量的垂直找到矛盾的条件,从而肯定点的不存在.
(2)先假设点Q存在,然后利用反证法进行证明,通过向量的垂直找到矛盾的条件,从而肯定点的不存在.
解答:
 解:(1)因为AB=2BC,∠ABC=60°,
解:(1)因为AB=2BC,∠ABC=60°,
在△ABC中,由余弦定理可得 AC=
BC,
所以 AC⊥BC. 又因为 FC⊥DC
平面CDEF⊥面ABCD,所以FC⊥平面ABCD.
所以CA,CF,CB两两互相垂直,
如图建立空间直角坐标系C-xyz.
设BC=1,所以C(0,0,0),A(
,0,0),B(0,1,0),D(
,-
,0),E(
,-
,1)
所以
=(
,-
,1),
=(
,0,0),
=(0,1,0).
设平面EAC的法向量为
=(x,y,z),则有
所以
取z=1,得
=(0,2,1)
设BC与平面EAC所成的角为θ,则,sinθ=|cos|<
,
>|=
=
所以 BC与平面EAC所成角的正弦值为
.
(2)线段ED上不存在点Q,使平面EAC⊥平面QBC.证明如下:
假设线段ED上存在点Q,设 Q(
,-
,t)(0≤t≤1),所以
=(
,-
,t).
设平面QBC的法向量为
=(a,b,c),则有
所以
取 c=1,得
=(-
t,0,1).
要使平面EAC⊥平面QBC,只需
•
=0,即 -
t×0+0×2+1×1=0,
此方程无解,所以线段ED上不存在点Q,使平面EAC⊥平面QBC.
 解:(1)因为AB=2BC,∠ABC=60°,
解:(1)因为AB=2BC,∠ABC=60°,在△ABC中,由余弦定理可得 AC=
| 3 |
所以 AC⊥BC. 又因为 FC⊥DC
平面CDEF⊥面ABCD,所以FC⊥平面ABCD.
所以CA,CF,CB两两互相垂直,
如图建立空间直角坐标系C-xyz.
设BC=1,所以C(0,0,0),A(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以
| CE |
| ||
| 2 |
| 1 |
| 2 |
| CA |
| 3 |
| CB |
设平面EAC的法向量为
| n |
|
所以
|
| n |
设BC与平面EAC所成的角为θ,则,sinθ=|cos|<
| CB |
| n |
|
| ||||
|
|
2
| ||
| 5 |
所以 BC与平面EAC所成角的正弦值为
2
| ||
| 5 |
(2)线段ED上不存在点Q,使平面EAC⊥平面QBC.证明如下:
假设线段ED上存在点Q,设 Q(
| ||
| 2 |
| 1 |
| 2 |
| CQ |
| ||
| 2 |
| 1 |
| 2 |
设平面QBC的法向量为
| m |
|
所以
|
| m |
| 2 | ||
|
要使平面EAC⊥平面QBC,只需
| m |
| n |
| 2 | ||
|
此方程无解,所以线段ED上不存在点Q,使平面EAC⊥平面QBC.
点评:本题考查的知识点:解三角形,利用垂直关系建立空间直角坐标系,法向量,法向量与直线的夹角,反证法在几何问题中的应用

练习册系列答案
相关题目
复数z=
的共轭复数在复平面上对应的点位于( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若椭圆x2+my2=1的离心率e∈(
,
),则m的取值范围是( )
| ||
| 3 |
| ||
| 2 |
| A、(1,2) | ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|