题目内容
函数y=
的定义域为 ．
| x2-x-2 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可得到结论．
解答：
解：要使函数f（x）有意义，则x2-x-2≥0
解得x≥2或x≤-1，
即函数的定义域为{x|x≥2或x≤-1}，
故答案为：{x|x≥2或x≤-1}
解得x≥2或x≤-1，
即函数的定义域为{x|x≥2或x≤-1}，
故答案为：{x|x≥2或x≤-1}
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知log2（x+y）=log2x+log2y，则x+y的最小值是（ ）
| A、1 | B、4 | C、8 | D、16 |
若集合M={a，b，c}则有（ ）
| A、{a}∈M | B、c∈M |
| C、b?M | D、c={c} |
复数z=
的共轭复数在复平面上对应的点位于（ ）
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
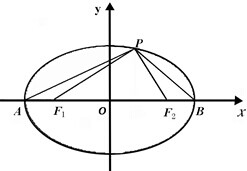如图，已知椭圆C：