题目内容
若△ABC的三条边的长度分别为a,b,c,则下列三组数据:①
,
,
②a2,b2,c2③lna,lnb,lnc中,一定能作为某三角形的三条边长的有( )
| a |
| b |
| c |
| A、0组 | B、1组 | C、2组 | D、3组 |
考点:命题的真假判断与应用
专题:解三角形,简易逻辑
分析:由△ABC的三条边的长度分别为a,b,c,不妨设a≤b≤c,则a+b>c.
①由(
+
)2-(
)2=a+b-c+2
>0,可得
+
>
,于是可知
,
,
能作为某三角形的三条边长.
②取a=2,b=3,c=4,但是22+32<42,即可判断出.
③lna,lnb,lnc,若取a=
,b=
,c=
,则lna<0,lnb<0,lnc<0.
①由(
| a |
| b |
| c |
| ab |
| a |
| b |
| c |
| a |
| b |
| c |
②取a=2,b=3,c=4,但是22+32<42,即可判断出.
③lna,lnb,lnc,若取a=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
解:由△ABC的三条边的长度分别为a,b,c,不妨设a≤b≤c,则a+b>c.
①∵(
+
)2-(
)2=a+b-c+2
>0,∴
+
>
,因此
,
,
一定能作为某三角形的三条边长.
②取a=2,b=3,c=4,但是22+32<42,因此a2,b2,c2不一定能作为某三角形的三条边长,不正确.
③lna,lnb,lnc,若取a=
,b=
,c=
,则lna<0,lnb<0,lnc<0,因此此时不能作为三角形的边长.
综上可得:一定能作为某三角形的三条边长的只有①.
故选:B.
①∵(
| a |
| b |
| c |
| ab |
| a |
| b |
| c |
| a |
| b |
| c |
②取a=2,b=3,c=4,但是22+32<42,因此a2,b2,c2不一定能作为某三角形的三条边长,不正确.
③lna,lnb,lnc,若取a=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
综上可得:一定能作为某三角形的三条边长的只有①.
故选:B.
点评:本题考查了不等式的性质、对数函数的性质、组成三角形三边的关系,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
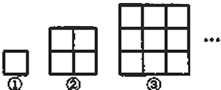 如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )
如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )| A、36 | B、55 | C、70 | D、91 |
有一个几何体的三视图如图所示,这个几何体是一个( )


| A、棱台 | B、棱锥 | C、棱柱 | D、圆台 |
平面α的一个法向量
=(1,-1,0),则y轴与平面α所成的角的大小为( )
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
极坐标平面内,集合P={(ρ,θ)|sinθ=-
,ρ∈R}与集合S={(ρ,θ)|cosθ=
,ρ∈R}之间的关系是( )
| 1 |
| 2 |
| ||
| 2 |
| A、P?S |
| B、P?S |
| C、P=S |
| D、P∩S={(0,0)} |
在空间内,设l,m,n是三条不同的直线,α,β,γ是三个不同的平面,则下列命题中为假命题的是( )
| A、α⊥γ,β⊥γ,α∩β=l,则l⊥γ |
| B、l∥α,l∥β,α∩β=m,则l∥m |
| C、α∩β=l,β∩γ=m,γ∩α=n,l∥m,则l∥n |
| D、α⊥γ,β⊥γ,则α⊥β或α∥β |
下列命题正确的个数是( )
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
| A、0 | B、1 | C、2 | D、3 |
已知不等式x2-x≤0的解集为M,且集合N={x|
<0},则M∩N为( )
| x+1 |
| x-1 |
| A、[0,1) |
| B、(0,1) |
| C、[0,1] |
| D、(-1,0] |
 如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为
如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为