题目内容
平面α的一个法向量
=(1,-1,0),则y轴与平面α所成的角的大小为( )
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:用空间向量求直线与平面的夹角
专题:计算题,空间角
分析:设y轴与平面α所成的角的大小为θ,由在y轴上的单位向量和平面α的一个法向量,利用向量法能求出结果.
解答:
解:设y轴与平面α所成的角的大小为θ,
∵在y轴上的单位向量
=(0,1,0),平面α的一个法向量
=(1,-1,0),
∴sinθ=|cos<
,
>|=|
|=
,
∴θ=
.
故选:B.
∵在y轴上的单位向量
| j |
| n |
∴sinθ=|cos<
| j |
| n |
| -1 | ||
1•
|
| ||
| 2 |
∴θ=
| π |
| 4 |
故选:B.
点评:本题考查直线与平面所成角的大小的求法,是基础题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
已知两条不同直线l,m以及△ABC,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( )
| A、相交 | B、平行 |
| C、异面 | D、以上都有可能 |
已知数列{an}满足a1=0,an+1=
(n∈N*),则a19=( )
an-
| ||
|
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
在空间直角坐标系中,点B是点A(2,-3,5)关于xOy面的对称点,则|AB|=( )
| A、10 | ||
B、
| ||
C、
| ||
| D、38 |
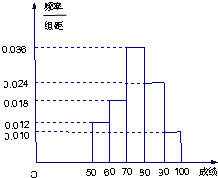 某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )
某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )| A、240 | B、560 |
| C、280 | D、420 |