题目内容
下列命题正确的个数是( )
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
(1)有两个面互相平行,其余各面都是平行四边形的几何体是棱柱
(2)棱柱的底面一定是平行四边形
(3)棱锥被平面分成的两部分不可能都是棱锥
(4)用平行于圆锥底面的平面去截这个圆锥,所得几何体叫做圆台.
| A、0 | B、1 | C、2 | D、3 |
考点:构成空间几何体的基本元素
专题:空间位置关系与距离
分析:根据多面体的性质和几何体的定义来判断,采用举反例的方法来以及对概念的理解进行否定.
解答:
解:(1)如图,有两个面互相平行,其余各面都是平行四边形的几何体,
但是这个几何体不是棱柱,∴(1)不正确.
(2)五棱柱的底面是五边形,六棱柱的底面是六边形,∴(2)不正确;
(3)棱锥被过顶点的平面分成的两部分有可能都是棱锥,∴(3)不正确;
(4)用平行于圆锥底面的平面去截这个圆锥,
底面与截面之间的部分叫圆台,∴(4)不正确.
故选:A.

但是这个几何体不是棱柱,∴(1)不正确.
(2)五棱柱的底面是五边形,六棱柱的底面是六边形,∴(2)不正确;
(3)棱锥被过顶点的平面分成的两部分有可能都是棱锥,∴(3)不正确;
(4)用平行于圆锥底面的平面去截这个圆锥,
底面与截面之间的部分叫圆台,∴(4)不正确.
故选:A.
点评:本题考查命题真假的判断,是基础题,准确理解几何体的定义,是真正把握几何体结构特征的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
化简
+
+
-
=( )
| AB |
| BD |
| CA |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
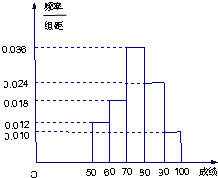 某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )
某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )| A、240 | B、560 |
| C、280 | D、420 |
已知x=
与x=
为函数f(x)=3sin(ωx+
)的两条相邻对称轴,则ω=( )
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
已知锐角三角形的边长分别是3,5,x,则x的取值范围是( )
A、1<x<
| ||
B、4<x<
| ||
| C、1<x<4 | ||
D、4<x<
|
以下棱柱中,最多只有一对面互相平行的是( )
| A、三棱柱 | B、四棱柱 |
| C、八棱柱 | D、六棱柱 |