题目内容
3.某日,甲乙二人随机选择早上6:00-7:00的某一时刻到达黔灵山公园早锻炼,则甲比乙提前到达超过20分钟的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | $\frac{2}{9}$ |
分析 设甲到校的时间为x,乙到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|0≤x≤60,0≤y≤60}是一个矩形区域,对应的面积S=60×60=3600,则甲比乙提前到达超过20分钟事件A={(x,y)|y-x≥5}对应的面积$\frac{1}{2}$×40×40=800,根据几何概率模型的规则求解即可.
解答 解:设甲到校的时间为x,乙到校的时间为y.
(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|0≤x≤60,0≤y≤60}是一个矩形区域,对应的面积S=60×60=3600,
则甲比乙提前到达超过20分钟事件A={x|y-x≥20},对应的面积$\frac{1}{2}$×40×40=800,
几何概率模型可知甲比乙提前到达超过20分钟的概率为$\frac{800}{3600}$=$\frac{2}{9}$.
故选:D.
点评 本题考查几何概率模型与模拟方法估计概率,求解的关键是掌握两种求概率的方法的定义及规则,求出对应区域的面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知tanα=$\frac{1}{3}$,则$\frac{sinα-co{s}^{3}α}{sinα+cosα}$=( )
| A. | -$\frac{17}{40}$ | B. | -$\frac{5}{16}$ | C. | -$\frac{34}{45}$ | D. | -$\frac{1}{2}$ |
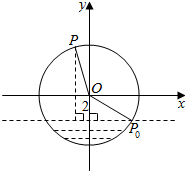 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.