题目内容
函数f(x)=
(a>0,b>0)的图象形如汉字“囧”,故称其为“囧函数”.给出下列五个命题:
①“囧函数”在在(0,+∞)上单调递增;
②“囧函数”的值域为R;
③“囧函数”有两个零点;
④“囧函数”的图象关于y轴对称;
⑤“囧函数”的图象与直线y=kx+m(k≠0)至少有一个交点.
其中正确的结论是: .(写出所有正确结论的序号)
| b |
| |x|-a |
①“囧函数”在在(0,+∞)上单调递增;
②“囧函数”的值域为R;
③“囧函数”有两个零点;
④“囧函数”的图象关于y轴对称;
⑤“囧函数”的图象与直线y=kx+m(k≠0)至少有一个交点.
其中正确的结论是:
考点:函数的图象
专题:函数的性质及应用
分析:先判断函数为偶函数,再令a=b=1,得到特殊的函数,利用特殊值法,研究函数的值域,单调性,和零点问题,利用数形结合的方法进行判断;
解答:
 解:(1)由题意,f(x)=
解:(1)由题意,f(x)=
(a>0,b>0),f(-x)=f(x),是偶函数;
当a=b=1时,
则f(x)=
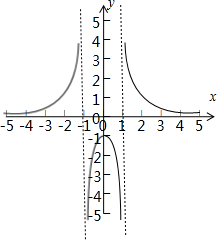
,其函数的图象如图:如图显然f(x)在(0,+∞)上不是单调函数,故①错误;
如图y≠0,值域肯定不为R,故②错误;
如图f(x)≠0,没有零点,故③错误;
f(x)是偶函数,关于y轴对称,故④正确;
如图可知函数f(x)的图象,x=1换为x=a,在四个象限都有图象,
此时与直线y=kx+b(k≠0)的图象至少有一个交点.故⑤正确;
故答案为:④⑤;
 解:(1)由题意,f(x)=
解:(1)由题意,f(x)=| b |
| |x|-a |
当a=b=1时,
则f(x)=
| 1 |
| |x|-1 |
如图y≠0,值域肯定不为R,故②错误;
如图f(x)≠0,没有零点,故③错误;
f(x)是偶函数,关于y轴对称,故④正确;
如图可知函数f(x)的图象,x=1换为x=a,在四个象限都有图象,
此时与直线y=kx+b(k≠0)的图象至少有一个交点.故⑤正确;
故答案为:④⑤;
点评:本题考查“囧函数”的新定义,关键要读懂题意,只要画出其图象就很容易求解了,解题过程中用到了数形结合的方法,属于基础题.

练习册系列答案
相关题目
抛物线y=-x2+6x-7的对称轴方程是直线( )
| A、x=6 | B、x=3 |
| C、x=-3 | D、x=-6 |
已知f(x)的图象关于原点对称,且x>0时,f(x)=-x2+1,则x<0时,f(x)=( )
| A、-x2+1 |
| B、-x2-1 |
| C、x2+1 |
| D、x2-1 |