题目内容
函数y=
+
的最小值为 ．
| x2+4x+5 |
| x2-4x+8 |
考点：函数的最值及其几何意义
专题：数形结合,函数的性质及应用
分析：函数y=
+
=
+
，
上式表示x轴上一点（x，0）到A（-2，1）和B（2，2）的和的最小值，画图利用数形结合解题．
| x2+4x+5 |
| x2-4x+8 |
| (x+2)2+(0-1)2 |
| (x-2)2+(0-2)2 |
上式表示x轴上一点（x，0）到A（-2，1）和B（2，2）的和的最小值，画图利用数形结合解题．
解答：
解：函数y=
+
=
+
，
上式表示x轴上一点（x，0）到A（-2，1）和B（2，2）的和的最小值，
如图：
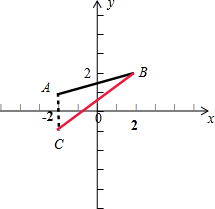
设C（-2，-1）为点A关于x轴的对称点，则当点（x，0）为直线BC与x轴的交点时，距离的和最小，最小值就是BC两点间的距离，
又|BC|=
=5
∴函数的最小值为5．
| x2+4x+5 |
| x2-4x+8 |
| (x+2)2+(0-1)2 |
| (x-2)2+(0-2)2 |
上式表示x轴上一点（x，0）到A（-2，1）和B（2，2）的和的最小值，
如图：
设C（-2，-1）为点A关于x轴的对称点，则当点（x，0）为直线BC与x轴的交点时，距离的和最小，最小值就是BC两点间的距离，
又|BC|=
| (-2-2)2+(-1-2)2 |
∴函数的最小值为5．
点评：本题主要考查函数求最值的方法，结合所给函数表达式的特点，利用数形结合解题是常用的方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}中，对任意n∈N*，a1+a2+…+an=2n-1，则a12+a22+…+an2等于（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|
已知点A（-1，1）、B（1，2）、C（-2，-1）、D（3，4），则向量
在
方向上的投影（ ）
| CD |
| AB |
A、
| ||||
B、3
| ||||
C、-
| ||||
D、-3
|
如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体的三视图，则该几何体体积的最小值等于（ ）| A、36 | ||
B、
| ||
| C、18 | ||
D、
|