题目内容
在△ABC中，三内角A，B，C的对边分别为a，b，c，且a2=b2+c2+bc，a=
，S为△ABC的面积，则S+
cosBcosC的最大值为 ．
| 3 |
| 3 |
考点：余弦定理
专题：三角函数的求值,解三角形
分析：先利用余弦定理求得A，进而通过正弦定理表示出c，代入面积公式求得S+
cosBcosC的表达式，利用两角和与差的余弦函数公式化简求得其最大值．
| 3 |
解答：
解：∵a2=b2+c2+bc，
∴cosA=
=-
，
∴A=
，
由正弦定理 c=a•
=
×
=2sinC，
∴S=
=
=
sinBsinC
∴S+
cosBcosC=
sinBsinC+
cosBcosC=
cos（B-C）≤
，
故答案为：
．
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
由正弦定理 c=a•
| sinC |
| sinA |
| 3 |
| sinC | ||||
|
∴S=
| acsinB |
| 2 |
| ||
| 2 |
| 3 |
∴S+
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
故答案为：
| 3 |
点评：本题主要考查了正弦定理和余弦定理的应用．求得面积的表达式是解决问题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知实数x，y满足约束条件
，则z=x+3y的最大值等于（ ）
|
| A、9 | B、12 | C、27 | D、36 |
若a∈R，则a=2是（a-1）（a-2）=0的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
将函数y=sin（2x-
）的图象向右平移
个单位，然后纵坐标不变横坐标伸长为原来的2倍，得到函数解析式为（ ）
| π |
| 3 |
| π |
| 12 |
A、y=sin（x-
| ||
| B、y=cosx | ||
| C、y=-cosx | ||
| D、y=-sinx |
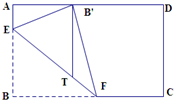如图，有一张长为8，宽为4的矩形纸片ABCD，按图所示的方法进行折叠，使每次折叠后点B都落在AD边上，此时将B记为B′（注：图中EF为折痕，点F也可落在边CD上），过B'做B′T∥CD交EF于T点，则T点的轨迹所在的曲线是（ ）