题目内容
将函数y=sin(2x-
)的图象向右平移
个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为( )
| π |
| 3 |
| π |
| 12 |
A、y=sin(x-
| ||
| B、y=cosx | ||
| C、y=-cosx | ||
| D、y=-sinx |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据三角函数图象变换的公式,结合诱导公式进行化简,可得两次变换后所得到的图象对应函数解析式.
解答:
解:设f(x)=sin(2x-
),可得y=f(x)的图象向右平移
,得到f(x-
)=sin[2(x-
)-
]=sin(2x-
)的图象,
再将所得的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),可得f(
x-
)=sin(x-
)=-cosx的图象.
∴函数y=sin(2x-
)的图象按题中的两步变换,最终得到的图象对应函数解析式为y=-cosx,
故选:C.
| π |
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
再将所得的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),可得f(
| 1 |
| 2 |
| π |
| 12 |
| π |
| 2 |
∴函数y=sin(2x-
| π |
| 3 |
故选:C.
点评:本题给出三角函数图象的平移和伸缩变换,求得到的图象对应的函数解析式.着重考查了三角函数图象的变换公式和诱导公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列
,
,2
,
,…,则2
是这个数列的( )
| 2 |
| 5 |
| 2 |
| 11 |
| 5 |
| A、第6项 | B、第7项 |
| C、第8项 | D、第9项 |
如图是某样本数据的茎叶图,则该样本数据的众数为( )
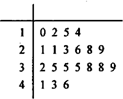

| A、10 | B、21 | C、35 | D、46 |
经过点(2,1),且倾斜角为135°的直线方程为( )
| A、x+y-3=0 |
| B、x-y-1=0 |
| C、2x-y-3=0 |
| D、x-2y=0 |
复数z=
,则z的共轭复数
在复平面内对应的点( )
| i2+i3+i4 |
| 1-i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |