题目内容
16.已知a>0,b>0,且a+b=2,则$\frac{1}{a}+\frac{2}{b}$的最小值为$\frac{3}{2}$+$\sqrt{2}$.分析 由题意整体代入可得$\frac{1}{a}+\frac{2}{b}$=$\frac{1}{2}$($\frac{1}{a}+\frac{2}{b}$)(a+b)=$\frac{1}{2}$(3+$\frac{b}{a}$+$\frac{2a}{b}$),由基本不等式可得.
解答 解:∵a>0,b>0,且a+b=2,
∴$\frac{1}{a}+\frac{2}{b}$=$\frac{1}{2}$($\frac{1}{a}+\frac{2}{b}$)(a+b)
=$\frac{1}{2}$(3+$\frac{b}{a}$+$\frac{2a}{b}$)≥$\frac{1}{2}$(3+2$\sqrt{2}$)=$\frac{3}{2}$+$\sqrt{2}$,
当且仅当$\frac{b}{a}$=$\frac{2a}{b}$即b=$\sqrt{2}$a时取等号,
结合a+b=2可解得a=2$\sqrt{2}$-2且b=4-2$\sqrt{2}$,
故答案为:$\frac{3}{2}$+$\sqrt{2}$.
点评 本题考查基本不等式求最值,整体代入并变形为可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.等差数列{an}中,a3=5,S6=36,则S9=( )
| A. | 17 | B. | 19 | C. | 81 | D. | 100 |
1.公比不为1的等比数列{an}满足a5a6+a4a7=18,若a1am=9,则m的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
6.已知a>b>m>0,则( )
| A. | $sin\frac{b-m}{a-m}<sin\frac{b+m}{a+m}<sin\frac{b}{a}$ | B. | $sin\frac{b-m}{a-m}>sin\frac{b+m}{a+m}>sin\frac{b}{a}$ | ||
| C. | $sin\frac{b-m}{a-m}>sin\frac{b}{a}>sin\frac{b+m}{a+m}$ | D. | $sin\frac{b-m}{a-m}<sin\frac{b}{a}<sin\frac{b+m}{a+m}$ |
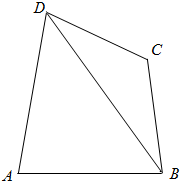 如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求
如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求