题目内容
7.在等腰直角△ABC中,AB=AC=4,点P是边AB上异于A、B的一点,光线从点P出发经过BC、CA反射后又回到点P,光线交线段BC于点Q,交线段CA于点R,若光线QR经过△ABC的重心,求线段AP的长度.分析 建立坐标系,可得直线方程和重心坐标,由反射原理可得P的两个对称点坐标,可得直线方程,进而可得P的坐标,可得AP长度.
解答 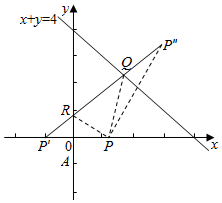 解:由题意建立如图所示的坐标系,则A(0,0),B(4,0),C(0,4),可得BC的方程为x+y=4,可得重心($\frac{4}{3}$,$\frac{4}{3}$)
解:由题意建立如图所示的坐标系,则A(0,0),B(4,0),C(0,4),可得BC的方程为x+y=4,可得重心($\frac{4}{3}$,$\frac{4}{3}$)
设P(a,0),则P关于AC即y轴的对称点P′(-a,0),
设P关于BC的对称点P″(m,n),则$\left\{\begin{array}{l}{\frac{m+a}{2}+\frac{n+0}{2}=4}\\{\frac{n-0}{m-a}•(-1)=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=4}\\{n=4-a}\end{array}\right.$,即P″(4,4-a),
∴光线QR即P′P″的方程为y=$\frac{4-a}{4+a}$(x+a),
代入($\frac{4}{3}$,$\frac{4}{3}$)可得$\frac{4}{3}$=$\frac{4-a}{4+a}$($\frac{4}{3}$+a),
解得a=$\frac{4}{3}$或a=0(舍去)
∴线段AP的长度为$\frac{4}{3}$
点评 本题考查直线和点的对称性,涉及光的反射原理和方程组的解法,属中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{cos(1-{x}^{2}),x<0}\\{-tan2x,x≥0}\end{array}\right.$,则f[f($\frac{π}{8}$)]=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
2.“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄(X)分别为16岁、18岁、20岁和22岁,其得肺癌的相对危险度(Y)依次为15.10、12.81、9.72、3.21;每天吸烟(U)10支、20支、30支者,其得肺癌的相对危险度(v)分别为7.5、9.5和16.6.用r1表示变量X与y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
| A. | rl=r2 | B. | r1>r2>0 | C. | 0<r1<r2 | D. | r1<0<r2 |
19.已知复数z满足z(1+i)=1(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |