题目内容
4.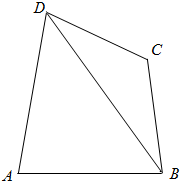 如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求
如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求(Ⅰ)BD;
(Ⅱ)∠ADB.
分析 (Ⅰ)在△BCD中,由已知及正弦定理即可计算求得BD=$\frac{CD•sin∠BCD}{sin∠CBD}$的值.
(Ⅱ)由已知及余弦定理可求cos∠ADB=$\frac{A{D}^{2}+B{D}^{2}-A{B}^{2}}{2AD•BD}$ 的值,即可得解∠ADB=45°.
解答 (本题满分为12分)
解:(Ⅰ)在△BCD中,由正弦定理得:$\frac{BD}{sin∠BCD}$=$\frac{CD}{sin∠CBD}$,…(3分)
故BD=$\frac{CD•sin∠BCD}{sin∠CBD}$=$\frac{\sqrt{3}×\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=3,…(6分)
(Ⅱ)在△ABD中,由余弦定理得:cos∠ADB=$\frac{A{D}^{2}+B{D}^{2}-A{B}^{2}}{2AD•BD}$ …(8分)
=$\frac{(2\sqrt{2})^{2}+{3}^{2}-(\sqrt{5})^{2}}{2×2\sqrt{2}×3}$=$\frac{\sqrt{2}}{2}$,…(10分)
所以∠ADB=45°. …(12分)
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{cos(1-{x}^{2}),x<0}\\{-tan2x,x≥0}\end{array}\right.$,则f[f($\frac{π}{8}$)]=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
19.已知复数z满足z(1+i)=1(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
9.函数$y=sin(2x-\frac{π}{3})$与$y=cos(2x+\frac{2π}{3})$的图象关于直线x=a对称,则a可能是( )
| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{11π}{24}$ |
13.设复数z满足(1+i)z=2,则z的共轭复数$\overline{z}$=( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
14.函数f(x)=log2(4x+1)的值域为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |