题目内容
6．等差数列{an}中，a3=5，S6=36，则S9=（ ）| A． | 17 | B． | 19 | C． | 81 | D． | 100 |
分析 由题意列关于首项和公差的方程组，求解方程组得首项和公差，代入等差数列的前n项和得答案．
解答 解：由a3=5，S6=36，得
$\left\{{\begin{array}{l}{{a_3}={a_1}+2d=5}\\{6{a_1}+\frac{6×5d}{2}=36}\end{array}}\right.$，解得$\left\{{\begin{array}{l}{{a_1}=1}\\{d=2}\end{array}}\right.$，
∴${S_9}=9{a_1}+\frac{9×8d}{2}=9{a_1}+36d=81$，
故选：C．
点评 本题考查等差数列的通项公式，考查了等差数列的前n项和，是基础题．
练习册系列答案
相关题目
1．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | $2\sqrt{3}$ | B． | $2\sqrt{2}$ | C． | $\sqrt{10}$ | D． | $\sqrt{13}$ |
11．
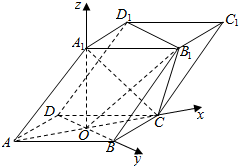如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=$\sqrt{2}$．平面OCB1的法向量$\overrightarrow{n}$=（x，y，z）为（ ）
如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=$\sqrt{2}$．平面OCB1的法向量$\overrightarrow{n}$=（x，y，z）为（ ）| A． | （0，1，1） | B． | （1，-1，1） | C． | （0，1，-1） | D． | （-1，-1，1） |