题目内容

1．公比不为1的等比数列{an}满足a5a6+a4a7=18，若a1am=9，则m的值为（　　）
A．8B．9C．10D．11

分析 由已知结合等比数列的性质可得a1a10=9，又a1am=9，得a1a10=a1am，从而得到m=10．

解答 解：在等比数列{an}中，由a5a6+a4a7=18，得2a1a10=18，
∴a1a10=9，又a1am=9，
∴a1a10=a1am，则m=10．
故选：C．

点评 本题考查等比数列的性质，是基础的计算题．

练习册系列答案
相关题目
11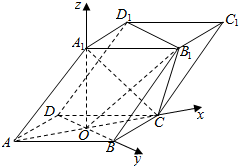．如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=$\sqrt{2}$．平面OCB1的法向量$\overrightarrow{n}$=（x，y，z）为（　　）
A．（0，1，1）B．（1，-1，1）C．（0，1，-1）D．（-1，-1，1）
12．已知定义在R上的函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的最小值为-2，其相邻两条对称轴距离为$\frac{π}{2}$，函数图象向左平移$\frac{π}{12}$单位后所得图象对应的函数为偶函数．
（1）求函数f（x）的解析式；
（2）若f（$\frac{{x}_{0}}{2}$）=-$\frac{3}{8}$，且x0∈[$\frac{π}{2}，π$]，求cos（x0+$\frac{π}{6}$）的值．
9．函数$y=sin（2x-\frac{π}{3}）$与$y=cos（2x+\frac{2π}{3}）$的图象关于直线x=a对称，则a可能是（　　）
A．$\frac{π}{24}$B．$\frac{π}{12}$C．$\frac{π}{8}$D．$\frac{11π}{24}$
16．已知a＞0，b＞0，且a+b=2，则$\frac{1}{a}+\frac{2}{b}$的最小值为$\frac{3}{2}$+$\sqrt{2}$．
6．定义在（-2，2）上的奇函数f（x）恰有3个零点，当x∈（0，2）时，f（x）=xlnx-a（x-1）（a＞0），则a的取值范围是{a|a≥2ln2，或a=1}．
13．设复数z满足（1+i）z=2，则z的共轭复数$\overline{z}$=（　　）
A．-1-iB．-1+iC．1-iD．1+i
10．在复平面内，复数$\frac{2+i}{2i}$对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
11．有下列命题：
①△ABC中，若$\frac{cosA}{cosB}=\frac{a}{b}$，则△ABC一定是等腰三角形
②二次函数y=ax2+bx+c为偶函数的充要条件是b=0
③$b=\sqrt{ac}是a，b，c成等比的$必要不充分条件
④$y=sinx+\frac{1}{sinx}（{0＜x＜\frac{π}{2}}）$的最小值是2．
⑤a，b，c成等差数列的充要条件是2b=a+c．
其中正确命题的序号是①②⑤．
（注：把你认为正确的命题的序号都填上）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网