题目内容
求证：（1+1）（1+
）（1+
）…（1+
）＞
．
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 2n+1 |
考点：数学归纳法
专题：点列、递归数列与数学归纳法
分析：直接利用数学归纳法的证明步骤，验证n=2时不等式成立，然后假设n=k时不等式成立，证明n=k+1时不等式也成立即可．
解答：
证明：（1）当n=1时，左边=1+1=2＞
=右边显然成立．（2分）
（2）假设n=k（k≥1且k∈N）时，：（1+1）（1+
）（1+
）…（1+
）＞
成立 （4分）
则当n=k+1时，（1+1）（1+
）（1+
）…（1+
）（1+
）＞
（1+
）=
+1． （5分）
又因为2
＞1，
∴(
+1)2=2k+2+2
＞2k+3，
即（1+1）（1+
）（1+
）…（1+
）（1+
）＞
，
当n=k+1时，不等式也成立．（11分）
由（1）（2）可知对于大于1的任意自然数n，都有（1+1）（1+
）（1+
）…（1+
）＞
（12分）
| 3 |
（2）假设n=k（k≥1且k∈N）时，：（1+1）（1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| 2k+1 |
则当n=k+1时，（1+1）（1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 2k+1 |
又因为2
| 2k+1 |
∴(
| 2k+1 |
| 2k+1 |
即（1+1）（1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1 |
| 2(k+1)+1 |
当n=k+1时，不等式也成立．（11分）
由（1）（2）可知对于大于1的任意自然数n，都有（1+1）（1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 2n+1 |
点评：本题考查数学归纳法证明不等式的证明步骤，注意n=k+1时必须用上假设，考查逻辑推理能力．
练习册系列答案
相关题目
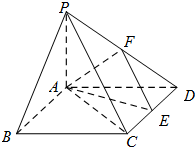如图在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=
如图，已知正方体ABCD-A1B1C1D1的棱长为2，M为正方形AA1D1D的中心，N为棱AB的中点．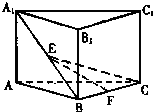
如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
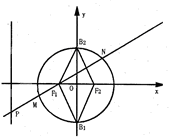如图，椭圆C：
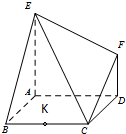如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，EA⊥底面ABCD，FD∥EA，且FD=