题目内容
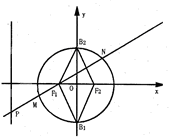 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)过左焦F1点的直线交椭圆于M、N两点,交直线x=-4于点P,设
| PM |
| MF1 |
| PN |
| NF2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设四边形F1B1F2B2的内切圆与边B2F2的切点为G,连接OG,则|OG|=
.由S△OB2F2利用等积法得bc=
a,e=
=
,由此能求出椭圆C的方程.
(Ⅱ)设直线MN的方程为y=k(x+1),代入椭圆方程,整理得 (3+4k2)x2+8k2x+4(k2-3)=0.由此利用韦达定理结合已知条件能证明λ+μ=0为定值.
| ||
| 2 |
| ||
| 2 |
| c |
| a |
| 1 |
| 2 |
(Ⅱ)设直线MN的方程为y=k(x+1),代入椭圆方程,整理得 (3+4k2)x2+8k2x+4(k2-3)=0.由此利用韦达定理结合已知条件能证明λ+μ=0为定值.
解答:
(Ⅰ)解:如图所示,设四边形F1B1F2B2的内切圆与边B2F2的切点为G,
连接OG,则|OG|=
.由S△OB2F2=
|OB2|•|OF2|=
|B2F2|•|OG|,
|OB2|=b,|OF2|=c,|B2F2|=a,
得bc=
a,又e=
=
,a2=b2+c2,解得a=2,b=
,
故椭圆C的方程为
+
=1.…(5分)
 (Ⅱ)证明:根据已知条件可设直线MN的方程为y=k(x+1),
(Ⅱ)证明:根据已知条件可设直线MN的方程为y=k(x+1),
代入椭圆方程,整理得 (3+4k2)x2+8k2x+4(k2-3)=0.
设M(x1,y1),N(x2,y2),则
.
又P(-4,-3k),由
=λ
,
=μ
,
得λ=-
,μ=-
.…(9分)
∴λ+μ=-
-
=-
=-
,
∵2x1x2+5(x1+x2)+8
=2•
+5(-
)+8
=
=0,
∴λ+μ=0为定值.…(13分)
连接OG,则|OG|=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|OB2|=b,|OF2|=c,|B2F2|=a,
得bc=
| ||
| 2 |
| c |
| a |
| 1 |
| 2 |
| 3 |
故椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
 (Ⅱ)证明:根据已知条件可设直线MN的方程为y=k(x+1),
(Ⅱ)证明:根据已知条件可设直线MN的方程为y=k(x+1),代入椭圆方程,整理得 (3+4k2)x2+8k2x+4(k2-3)=0.
设M(x1,y1),N(x2,y2),则
|
又P(-4,-3k),由
| PM |
| MF1 |
| PN |
| NF1 |
得λ=-
| x1+4 |
| x1+1 |
| x2+4 |
| x2+1 |
∴λ+μ=-
| x1+4 |
| x1+1 |
| x2+4 |
| x2+1 |
=-
| 2x1x2+5(x1+x2)+8 |
| (x1+1)(x2+1) |
=-
| 2x1x2+5(x1+x2)+8 |
| (x1+1)(x2+1) |
∵2x1x2+5(x1+x2)+8
=2•
| 4(k2-3) |
| 3+4k2 |
| -8k2 |
| 3+4k2 |
=
| 8k2-24-40k2+32k2+24 |
| 3+4k2 |
∴λ+μ=0为定值.…(13分)
点评:本题考查椭圆方程的求法,考查两数和为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
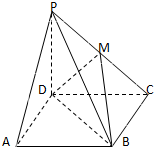 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点. 如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,EB=
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,EB=