题目内容

如图，已知正方体ABCD-A1B1C1D1的棱长为2，M为正方形AA1D1D的中心，N为棱AB的中点．
（Ⅰ）求证：MN∥平面BB1D1D；
（Ⅱ）求四棱锥N-BB1D1D的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：综合题,空间位置关系与距离
分析：（Ⅰ）取AD中点O，连接OM，ON，证明OM∥D1D，ON∥BD，可得平面MON∥平面BB1D1D，即可证明MN∥平面BB1D1D；
（Ⅱ）求出N到平面BB1D1D的距离，即可求四棱锥N-BB1D1D的体积．
解答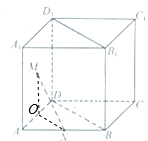： （Ⅰ）证明：取AD中点O，连接OM，ON，
∵M为正方形AA1D1D的中心，N为棱AB的中点，
∴OM∥D1D，ON∥BD，
∵OM∩ON=O，D1D∩BD=D，
∴平面MON∥平面BB1D1D，
∵MN?平面MON，
∴MN∥平面BB1D1D；
（Ⅱ）解：N到平面BB1D1D的距离为
2
4
•2=
2
2
，
∴四棱锥N-BB1D1D的体积为
1
3
•
2
•2•
2
2
=
2
3
．
点评：本题考查线面平行，考查四棱锥N-BB1D1D的体积，正确运用面面平行的判定与性质定理是关键．
练习册系列答案
相关题目
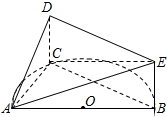如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC⊥平面ABC，DC∥BE，CD=BE，AB=4，tan∠EAB=
1
4
．
（1）证明：平面ADE⊥平面ACD；
（2）试探究当C在什么位置时三棱锥C-ADE的体积取得最大值，请说明理由并求出这个最大值．
已知函数f（x）=
a
x
+2lnx-1，a∈R．
（Ⅰ）当a=1时，求函数f（x）的单调区间；
（Ⅱ）求函数f（x）在区间（0，e]上的最小值．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，离心率为为
2
2
．点P在椭圆E上，且△PF1F2的周长为4
2
+4．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若直线l：y=x+m与椭圆E交于A，B两点，O为坐标原点，求△AOB面积的最大值．
设函数f（x）=
ex-e-x
2
，g（x）=
ex+e-x
2
，求证：g（2x）=[g（x）]2+[f（x）]2．
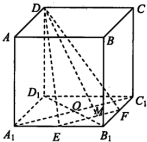如图，在正方形ABCD=A1B1C1D1中，AB=2，O为底面正方形A1B1C1D1的中心，E、F分别为A1B1、B1C1的中点，点M为EF上一点，且满足
EM
=
2
3
EF
，P为正方体底面ABCD上的点．
（Ⅰ）求证：平面DEF⊥平面BB1DD1．
（Ⅱ）若OP与DM相交，试判断OM与DP的位置关系；
（Ⅲ）在（Ⅱ）的条件下，求平面CDP与平面DPO所成锐二面角的大小为θ，求cosθ
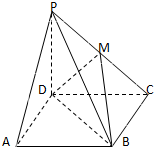在四棱锥P-ABCD中，侧棱PD⊥底面ABCD，底面ABCD是正方形，若PD=DA，M是PC的中点．
（Ⅰ）证明：PA∥平面BDM
（Ⅱ）若PD=
2
，求点C到平面BDM的距离．
求证：（1+1）（1+
1
3
）（1+
1
5
）…（1+
1
2n-1
）＞
2n+1
．
给定正整数k≥3，若项数为k的数列{an}满足：对任意的i=1、2、…、k，均有ai≤
Sk
k-1
（其中Sk=a1+a2+…+ak），则称数列{an}为“Γ数列”．
（Ⅰ）判断数列-1，3，5，2，4和
3
4
，
32
42
，
33
43
是否是“Γ数列”，并说明理由；
（Ⅱ）若{an}为“Γ数列”，求证：ai≥0对i=1，2，…，k恒成立；
（Ⅲ）设{bn}是公差为d的无穷项等差数列，若对任意的正整数m≥3，b1，b2，…，bm均构成“Γ数列”，求{bn}的公差d．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网