题目内容
为了了解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12．
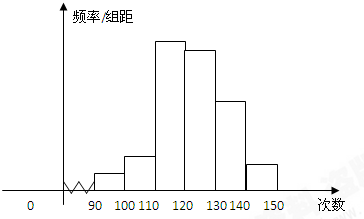
（1）第二小组的频率是多少？样本容量是多少？
（2）若次数在110以上（含110次）为达标，试估计该学校全体高一的学生达标的概率；
（3）为了分析学生的体能与身高，体重等方面的关系，必须再从样本中按分层抽样方法抽出50人作进一步分析，则体能在[120，130）的这段应抽多少人？
（1）第二小组的频率是多少？样本容量是多少？
（2）若次数在110以上（含110次）为达标，试估计该学校全体高一的学生达标的概率；
（3）为了分析学生的体能与身高，体重等方面的关系，必须再从样本中按分层抽样方法抽出50人作进一步分析，则体能在[120，130）的这段应抽多少人？
考点：频率分布直方图,分层抽样方法
专题：计算题,综合题,概率与统计
分析：（1）第二小组的频率是第二小组在整体中的比重，样本容量=
；
（2）用频率估计概率；
（3）求出体能在[120，130）的人数，再用分层抽样抽取体能在[120，130）的这段的人数．
| 频数 |
| 频率 |
（2）用频率估计概率；
（3）求出体能在[120，130）的人数，再用分层抽样抽取体能在[120，130）的这段的人数．
解答：
解：（1）第二小组频率为：
=0.08，
样本容量为：
=150．
（2）
=0.88．
（3）
×150×
=15．
| 4 |
| 2+4+17+15+9+3 |
样本容量为：
| 12 |
| 0.08 |
（2）
| 17+15+9+3 |
| 2+4+17+15+9+3 |
（3）
| 15 |
| 2+4+17+15+9+3 |
| 50 |
| 150 |
点评：本题考查了频率分布直方图的应用及分层抽样的方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目