题目内容
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组得到的频率分布表如下:
(1)为了能选拔出优秀的学生,高校决定在笔试成绩高的第三、四、五组中用分层抽样法抽取6名学生进入第二轮面试,试确定a,b,c的值并求第三、四、五组每组各抽取多少名学生进入第二轮面试;
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组中至少有一名学生被A考官面试的概率.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.050 |
| 第二组 | [165,170) | a | 0.350 |
| 第三组 | [170,175) | 30 | b |
| 第四组 | [175,180) | c | 0.200 |
| 第五组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组中至少有一名学生被A考官面试的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:本题的关键是找到频率分布直方图每一组的频数,在根据古典概型的计算公式求得概率.
解答:
解:(1)由频率分布表知a=100×0.35=35,b=
=0.3,c=100×0.2=20
因为第三、四、五组共有60名学生,所以利用分层抽样法在60名学生中抽取6名学生,每组分别为:第三组
×6=3人,第四组
×6=2人,第五组
×6=1人.
所以第三、四、五组分别抽取3人、2人、1人进入第二轮面试.
(2)设第三组的3名学生为A1、A2、A3,第四组的2名学生为B1、B2,
第五组的1名学生为C1.则从6名学生中抽取2名学生有15种可能:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2、C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),
第四组的2名学生至少有一名学生被A考官面试共有9种可能
其中第四组的2名学生至少有一名学生被A考官面试的概率为
=
.
| 30 |
| 100 |
因为第三、四、五组共有60名学生,所以利用分层抽样法在60名学生中抽取6名学生,每组分别为:第三组
| 30 |
| 60 |
| 20 |
| 60 |
| 10 |
| 60 |
所以第三、四、五组分别抽取3人、2人、1人进入第二轮面试.
(2)设第三组的3名学生为A1、A2、A3,第四组的2名学生为B1、B2,
第五组的1名学生为C1.则从6名学生中抽取2名学生有15种可能:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2、C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),
第四组的2名学生至少有一名学生被A考官面试共有9种可能
其中第四组的2名学生至少有一名学生被A考官面试的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考察频率分布直方图、分层抽样、古典概型的基本知识,是一道常见的高考题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
设α、β是两个不重合的平面,m、n是两条不重合的直线,则以下结论错误的是( )
| A、若α∥β,m?α,则 m∥β |
| B、若m∥α,m∥β,α∩β=n,则 m∥n |
| C、若m?α,n?α,m∥β,n∥β,则α∥β |
| D、若m∥α,m⊥β,则α⊥β |
已知变量x,y满足约束条件
,若x+2y≥-5恒成立,则实数a的取值范围为( )
|
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[-1,1] |
| D、[-1,1) |
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | ||
| B、若命题p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题. | ||
| C、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
D、“sinθ=
|
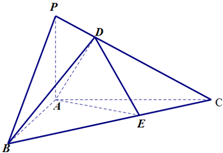 如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.
如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.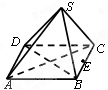 如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持
如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持