题目内容
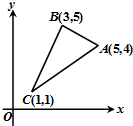 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是考点:简单线性规划
专题:不等式的解法及应用
分析:根据目标函数的几何意义,利用数形结合即可得到目标函数的斜率和三角形各边对应直线的斜率之间的关系即可得到结论.
解答:
解:由z=kx+y得y=-kx+z,
则直线y=-kx+z的截距最大时,z最大.
由图象知kBC=
=
=2,kAB=
=-
,
若直线斜率-k>0,即k<0,
要使目标函数z=kx+y当且仅当在点B处取得最大值,
则满足-k<kBC,即-k<2,
解得-2<k<0,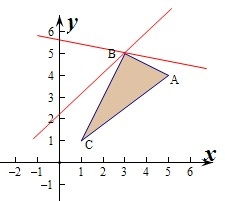
当k=0时,y=z,此时满足条件,
若-k<0时,即k>0,使目标函数z=kx+y当且仅当在点B处取得最大值,
则满足-k>kAC,即-k>-
,
即0<k<
,
综上-2<k<
,
故答案为:(-2,
);
则直线y=-kx+z的截距最大时,z最大.
由图象知kBC=
| 5-1 |
| 3-1 |
| 4 |
| 2 |
| 5-4 |
| 3-5 |
| 1 |
| 2 |
若直线斜率-k>0,即k<0,
要使目标函数z=kx+y当且仅当在点B处取得最大值,
则满足-k<kBC,即-k<2,
解得-2<k<0,

当k=0时,y=z,此时满足条件,
若-k<0时,即k>0,使目标函数z=kx+y当且仅当在点B处取得最大值,
则满足-k>kAC,即-k>-
| 1 |
| 2 |
即0<k<
| 1 |
| 2 |
综上-2<k<
| 1 |
| 2 |
故答案为:(-2,
| 1 |
| 2 |
点评:本题主要考查线性规划的应用,利用数形结合,是解决线性规划问题的基本方法.

练习册系列答案
相关题目
某几何体三视图如下图所示,则该几何体的体积是( )


A、1+
| ||
B、1+
| ||
C、1+
| ||
| D、1+π |
设a,b∈R,则“(a-b)a2>0”是“a>b”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |