题目内容
已知双曲线标准方程为
-x2=1，则双曲线离心率为（ ）
| y2 |
| 2 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用双曲线的性质直接求解．
解答：
解：∵双曲线标准方程为
-x2=1，
∴a=
，c=
，
∴e=
=
=
．
故选：C．
| y2 |
| 2 |
∴a=
| 2 |
| 3 |
∴e=
| c |
| a |
| ||
|
| ||
| 2 |
故选：C．
点评：本题考查双曲线的离心率的求法，是基础题，解题时要熟练掌握双曲线的简单性质．
练习册系列答案
阅读快车系列答案
相关题目
设a，b∈R，则“（a-b）a2＞0”是“a＞b”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
在△ABC中，角A、B、C的对边分别是a、b、c．若asinA+csinC-
asinC=bsinB．则角B等于（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设α、β是两个不重合的平面，m、n是两条不重合的直线，则以下结论错误的是（ ）
| A、若α∥β，m?α，则 m∥β |
| B、若m∥α，m∥β，α∩β=n，则 m∥n |
| C、若m?α，n?α，m∥β，n∥β，则α∥β |
| D、若m∥α，m⊥β，则α⊥β |
已知变量x，y满足约束条件
，若x+2y≥-5恒成立，则实数a的取值范围为（ ）
|
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、[-1，1] |
| D、[-1，1） |
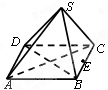如图，正四棱锥S-ABCD中，AB=2，E是边BC的中点，动点P在四棱锥的表面上运动，且总保持