题目内容
(ax-
)10的展开式中x4项的系数为210,则实数a的值为 .
| 1 | ||
|
考点:二项式系数的性质
专题:计算题,二项式定理
分析:在(ax-
)10的展开式的通项中,令x的指数为4,求出r值,再表示出x4项的系数,解关于a的方程即可.
| 1 | ||
|
解答:
解:(ax-
)10的展开式的通项为(-1)r a 10-r C10 rx10-
r,
令10-
r=4得r=4,
∴展开式中x4项的系数(-1)4 a6C104=210a6=210,
∴a=±1,
故答案为:±1.
| 1 | ||
|
| 3 |
| 2 |
令10-
| 3 |
| 2 |
∴展开式中x4项的系数(-1)4 a6C104=210a6=210,
∴a=±1,
故答案为:±1.
点评:本题考查二项式定理的应用,解决指定项的系数问题.牢记定理是前提,准确计算是关键.

练习册系列答案
相关题目
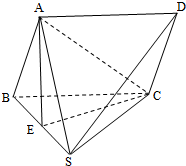 如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.
如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.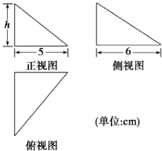 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=
图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=