题目内容
在直角坐标系xOy中,已知圆C1:(x-2)2+(y-2)2=4,动圆C2过点(2,0)和(-2,0),记两圆的交点为A、B,
(1)如果直线AB的方程为x-y-2=0,求圆C2的方程;
(2)设M为线段AB的中点,求|OM|的最大值.
(1)如果直线AB的方程为x-y-2=0,求圆C2的方程;
(2)设M为线段AB的中点,求|OM|的最大值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)联立AB的方程和圆C:(x-2)2+(y-2)2=4,可求得A和B的坐标,求出点(2,0)和(-2,0)构成弦的中垂线为x=0,弦AB的中垂线方程为y=-x+4,联立解得C2的圆心坐标为(0,4),由此写出C2的方程;
(2)假设B点坐标为(2+2cosθ,2+2sinθ),M为AB中点,则有M点坐标为(2+cosθ,1+sinθ),求出OM2的最大值,即可求|OM|的最大值.
(2)假设B点坐标为(2+2cosθ,2+2sinθ),M为AB中点,则有M点坐标为(2+cosθ,1+sinθ),求出OM2的最大值,即可求|OM|的最大值.
解答:
解:(1)联立AB的方程和圆C:(x-2)2+(y-2)2=4,可求得A和B的坐标分别为(2,0)和(4,2)
因为圆心在弦的中垂线上,点(2,0)和(-2,0)构成弦的中垂线为x=0
弦AB的中垂线方程为y=-x+4
联立解得C2的圆心坐标为(0,4),由此写出C2的方程为x2+(y-4)2=20
(2)因为B在圆C1上,假设B点坐标为(2+2cosθ,2+2sinθ)
M为AB中点,则有M点坐标为(2+cosθ,1+sinθ)
OM2=(2+cosθ)2+(1+sinθ)2=4+4cosθ+cos2θ+1+2sinθ+sin2θ
=6+4cosθ+2sinθ=6+2
sin(θ+α) 这里的α=arcsin
,
所以可知OM2的最大值为6+2
,
所以|OM|max=1+
.
因为圆心在弦的中垂线上,点(2,0)和(-2,0)构成弦的中垂线为x=0
弦AB的中垂线方程为y=-x+4
联立解得C2的圆心坐标为(0,4),由此写出C2的方程为x2+(y-4)2=20
(2)因为B在圆C1上,假设B点坐标为(2+2cosθ,2+2sinθ)
M为AB中点,则有M点坐标为(2+cosθ,1+sinθ)
OM2=(2+cosθ)2+(1+sinθ)2=4+4cosθ+cos2θ+1+2sinθ+sin2θ
=6+4cosθ+2sinθ=6+2
| 5 |
| 2 | ||
|
所以可知OM2的最大值为6+2
| 5 |
所以|OM|max=1+
| 5 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查参数法的运用,属于中档题.

练习册系列答案
相关题目
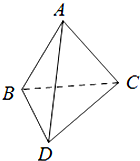 如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )
如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )