题目内容
已知O为坐标原点,P为圆x2+y2=20上的动点,过P作直线l垂直x轴于点Q,点M满足
=
(1)求动点M的轨迹C的方程
(2)若直线l:y=x+m(m≠0)与曲线C交于A,B两点,求三角形OAB面积的最大值.
| QP |
| 2 |
| QM |
(1)求动点M的轨迹C的方程
(2)若直线l:y=x+m(m≠0)与曲线C交于A,B两点,求三角形OAB面积的最大值.
考点:轨迹方程,函数的最值及其几何意义
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)确定坐标之间的关系,利用代入法求动点M的轨迹C的方程
(2)y=x+m代入x2+2y2=20,利用弦长公式求出|AB|,利用点到直线的距离公式求出O到直线l:y=x+m的距离,表示出三角形OAB面积,利用配方法求三角形OAB面积的最大值.
(2)y=x+m代入x2+2y2=20,利用弦长公式求出|AB|,利用点到直线的距离公式求出O到直线l:y=x+m的距离,表示出三角形OAB面积,利用配方法求三角形OAB面积的最大值.
解答:
解:(1)设M(x,y),P(a,b),则Q(a,0),
∵
=
,
∴(0,b)=
(a-x,-y),
∴a=x,b=-
y,
∵a2+b2=20,
∴x2+2y2=20;
(2)y=x+m代入x2+2y2=20,整理可得3x2+4mx+2m2-20=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
m,x1x2=
∴|AB|=
•
,
∵O到直线l:y=x+m的距离为
,
∴三角形OAB面积为
×
•
×
=
•
≤
×15=5
,
∴三角形OAB面积的最大值为5
.
∵
| QP |
| 2 |
| QM |
∴(0,b)=
| 2 |
∴a=x,b=-
| 2 |
∵a2+b2=20,
∴x2+2y2=20;
(2)y=x+m代入x2+2y2=20,整理可得3x2+4mx+2m2-20=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
| 4 |
| 3 |
| 2m2-20 |
| 3 |
∴|AB|=
| 2 |
|
∵O到直线l:y=x+m的距离为
| |m| | ||
|
∴三角形OAB面积为
| 1 |
| 2 |
| 2 |
|
| |m| | ||
|
| ||
| 3 |
| -m4+30m2 |
| ||
| 3 |
| 2 |
∴三角形OAB面积的最大值为5
| 2 |
点评:本题考查曲线方程的求法,考查三角形面积的最大值的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
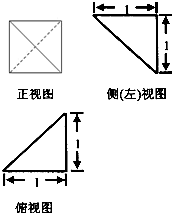
一个四面体的三视图如图所示,则该四面体的四个面中最大的面积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),若f(-1)>-2,f(-7)=
,则实数a的取值范围为( )
| a+1 |
| 3-2a |
A、(-
| ||
| B、(-2,1) | ||
C、(1,
| ||
D、(-∞,1)∪(
|
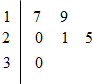 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.