题目内容
在极坐标系中,曲线ρ=2sinθ与ρsinθ-ρcosθ=2相交于点A、B两点,则|AB|= .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把圆与直线的极坐标方程化为直角坐标方程,利用点到直线的距离公式可得圆心C到直线的距离d.再利用弦长公式可得|AB|=2
.
| r2-d2 |
解答:
解:曲线ρ=2sinθ化为ρ2=2ρsinθ,∴x2+y2=2y,配方为x2+(y-1)2=1,可得圆心C(0,1),半径r=1.
ρsinθ-ρcosθ=2化为y-x=2,即x-y+2=0.
则圆心C到直线的距离d=
=
.
∴|AB|=2
=2
=
.
故答案为:
.
ρsinθ-ρcosθ=2化为y-x=2,即x-y+2=0.
则圆心C到直线的距离d=
| |0-1+2| | ||
|
| ||
| 2 |
∴|AB|=2
| r2-d2 |
1-(
|
| 2 |
故答案为:
| 2 |
点评:本题考查了把圆与直线的极坐标方程化为直角坐标方程、点到直线的距离公式、弦长公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
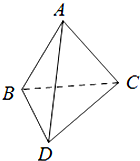 如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )
如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )
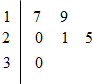 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.